#Введение
Данная статья является сборником всех моих постов про fopply из телеграма. Собрал в одном месте чтобы было удобнее читать, информация не потерялась и индексировалось поисковиками.
Каждый отдельный пост указывается датой публикации. После заголовка есть ссылка на посты в телеграме откуда это было взято.
#12.03.2020
Сегодня с утра у меня появилось непреодолимое желание написать частичку калькулятора над формулами. Его суть: у нас есть формулы и выражения. Мы можем применять формулы к выражениям, чтобы преобразовывать их к другому виду.
Я накидал программу, которая парсит формулы и выражения из строк и выполняет это "применение формулы".
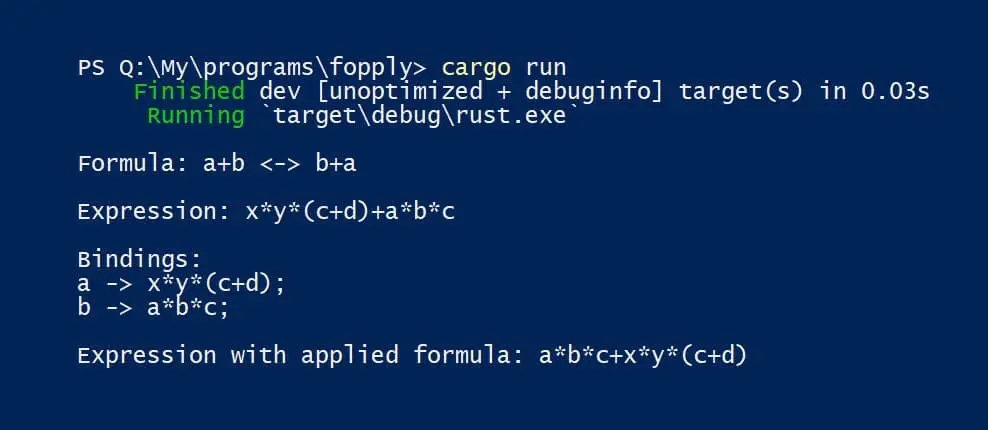
Например, у нас есть формула:
a+b <-> b+a
где символ <-> означает, что мы можем преобразовывать как левое в правое, так и наоборот.
Тогда если применить эту формулу к выражению:
x*y*(c+d) + a*b*c
то мы получим:
a*b*c + x*y*(c+d)
Что, собственно, моя программа и делает.
Вот код. Получилось немного: 168 строк кода.
Для представления выражения я использовал следующий enum:
enum Tree {
Function {
name: String,
args: Vec<Tree>,
},
Variable {
name: String,
}
}
Где Function::name может принимать значения "+", "*", "sin" и вообще любой функции.
Сначала при помощи rust-peg я паршу строку формулы в эту структуру данных.
Затем есть функция find_bindings, которая принимает формулу и выражение, и возвращает какие переменные в формулы соответствуют под-выражениям из основного выражения. Лучше всего это показать на примере:
find_bindings("a+b", "x*y*(c+d) + a*b*c") ->
[
("a", "x*y*(c+d)"),
("b", "a*b*c")
]
Потом имеется функция apply, которая берёт эти биндинги и вторую часть формулы, и заменят в формуле все вхождения переменных на выражения:
apply("b+a", bindings) -> "a*b*c + x*y*(c+d)"
По сути эти две функции являются ядром всех вычислений. Они написаны в функциональном и рекурсивном стиле, что получилось очень прикольно, но при этом и страшно (для непосвящённых).
В качестве дальнейшего развития:
- хочу сделать возможность из одних формул выводить другие,
- запись всего этого в текстовом файле (см.
formulas.txt) - дорасти до функционала моего старого проекта по преобразованию выражений (про который дай бог расскажу потом)
jpg
#15.03.2020
Итак, в своей проге-калькуляторе я добавил грамматику, чтобы парсилось вычитание и деление, затем улучшил вывод формул.
Раньше у меня формула могла примениться только к самому выражению, а не к какой-то внутренней его части.
Тогда я написал функцию, которая применят формулу где-то внутри выражения, рекурсивно пробегаясь по нему.
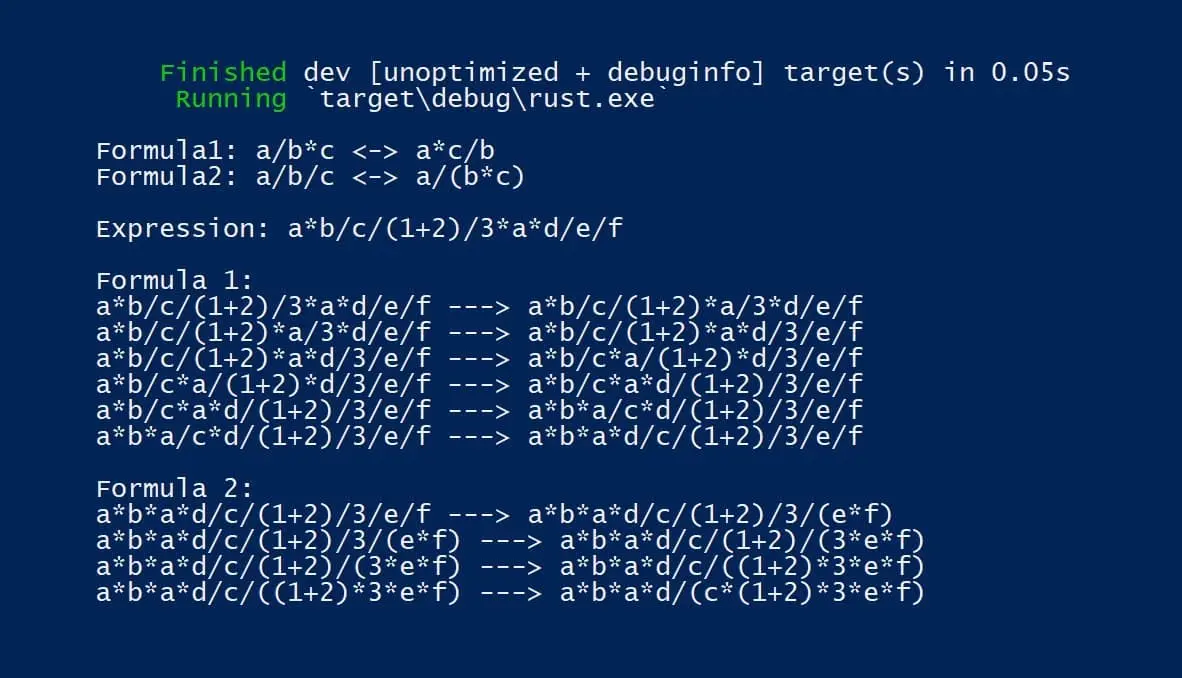
Затем я взял такие формулы:
a/b*c <-> a*c/ba/b/c <-> a/(b*c)
Где первая, очевидно, позволяет перемещать делящийся аргумент в выражении вправо.
А вторая позволяет объединять два делящихся аргумента в один.
Затем я взял выражение:
a*b/c/(1+2)/3*a*d/e/f
Так вот, сначала я заставил программу применять первую формулу до тех пор, пока она применяется, получилось вот это:
a*b*a*d/c/(1+2)/3/e/f
Затем я заставил аналогичным образом применяться вторую формулу, и в итоге получилось:
a*b*a*d/(c*(1+2)*3*e*f)
В общем, при помощи двух простых формул я получил программу, которая может произвольное выражение с делением и умножением привести к виду с одним числителем и знаменателем!!! \0/
jpg
Я добавил ещё кучу формул:
Преобразование к дроби:
a/b*c <-> a*c/b
a/b/c <-> a/(b*c)
Сложение дробей:
a/b + c/d <-> (a*d+c*b)/(b*d)
a + c/d <-> (a*d+c)/d
a/b + c <-> (a+c*b)/b
Раскрытие скобок:
c*(a+b) <-> (a+b)*c
(a+b)*c <-> a*c+b*c
Простейшая оптимизация:
1*a <-> a
a*1 <-> a
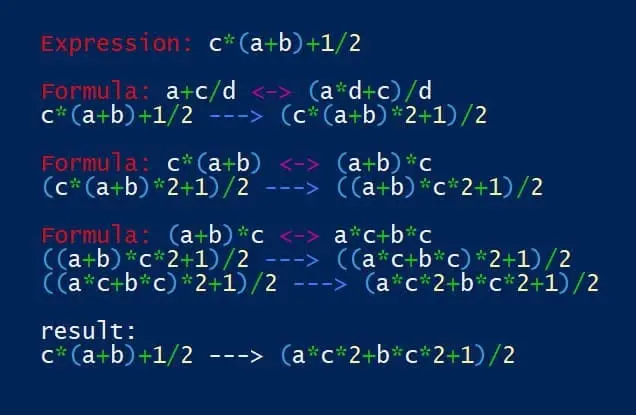
И заставил их все применяться к выражению:
c*(a+b)+1/2
В итоге программа привела его к виду:
(2ac + 2bc + 1)/2
!!! 🎉 !!!
(специально преобразовал к более читабельному виду, убрал лишние умножения)
В общем она научилась раскрывать скобки и складывать дроби!
Вот ещё примеры работы:
1/(a+b)+1/(c+d) ---> (c+d+a+b)/(ca+da+cb+db)
(x+1)*(x+2) ---> x*x + 2x + x + 2
Конечно, она ещё плохо работает на некоторых примерах, и за счёт внутреннего представления выражения, и за счёт того что надо прикручивать дополнительную логику, но результаты уже впечатляют!
jpg
Я тут значит мучаюсь с арифметической грамматикой, а в либе, которую я использую, уже есть средства для работы с парсингом чего-то где есть приоритет операций!

jpg
Заметьте, как расставлены скобочки вокруг @, они отличаются только для ^, потому что:
a-b-c = (a-b)-c
a^b^c = a^(b^c)
#16.03.2020
Тем временем:
- Перевёл весь возможный парсинг на precedence!{}, описанный в предыдущем сообщении.
- Добавил парсинг фукций вида f(a, b, c, ...)
- Добавил парсинг
- a & b - логических функций
- a = b - равенства, неравенства Но это не так интересно, и можно будет увидеть на следующем скриншоте.
А чтобы в этом посте было что-то интересно, я опишу вам крутые функции, на которых будет много чего строиться в будущем!
Для начала договоримся считать операции +, -, * итд как функции от двух аргументов:
a+b = sum(a, b)
a-b-c = sub(sub(a, b), c)
#2Функция many
Эта функция принимает на вход два чего угодно одного типа, и она означает, что два значения существуют параллельно. Свойства у неё такие, что, находясь в любой функции, она может из неё выйти. Лучше показать на примере:
1+many(1, 2) = many(1+1, 1+2)
sin(many(pi, 0)) = many(sin(pi), sin(0))
#2Функция ifval
Первый аргумент этой функции - некоторое выражение; а второй - логическое условие. Эта функция позволяет задавать значение, которое существует только при каком-то условии. В его свойства тоже входит, что она может выходить почти из любой функции (пока не знаю, как она должна выходить из логических функций). Опять же пример наше всё:
1+ifval(a, a != 0) = ifval(1+a, a != 0)
При помощи комбинации этих двух функций, можно определить множество интересных вещей, например, модуль!
abs(x) = many(ifval(x, x >= 0), ifval(-x, x < 0))
Или корни квадратного уравнения:
x = (-b + many(D, -D))/(2a)
Либо безопасное добавление новых переменных. Чтобы объяснить это, давайте вспомним, как мы иногда на математике решали примеры: добавляли в конце прибавление и отнимание какого-то выражения:
a = a+b-b
Затем использовали это, например, чтобы выделить полный квадрат:
x+2x = x+2x + 1 - 1 = (x+1)^2 - 1
С добавлением умножения и деления не всё так просто, ведь мы можем случайно умножить и поделить на ноль! Поэтому формула добавления умножения выглядит так:
a <-> many(ifval(a, b == 0), ifval(b*a/b, b != 0))
Благодаря этой формуле мы можем безопасно производить дальнейшие вычисления и ничего не потерять или не сломать. Ещё эта формула работает в обе стороны.
Стандартная формула работает в одну сторону, соответственно ломает эквивалентность входа и выхода:
a -> b*a/b
png
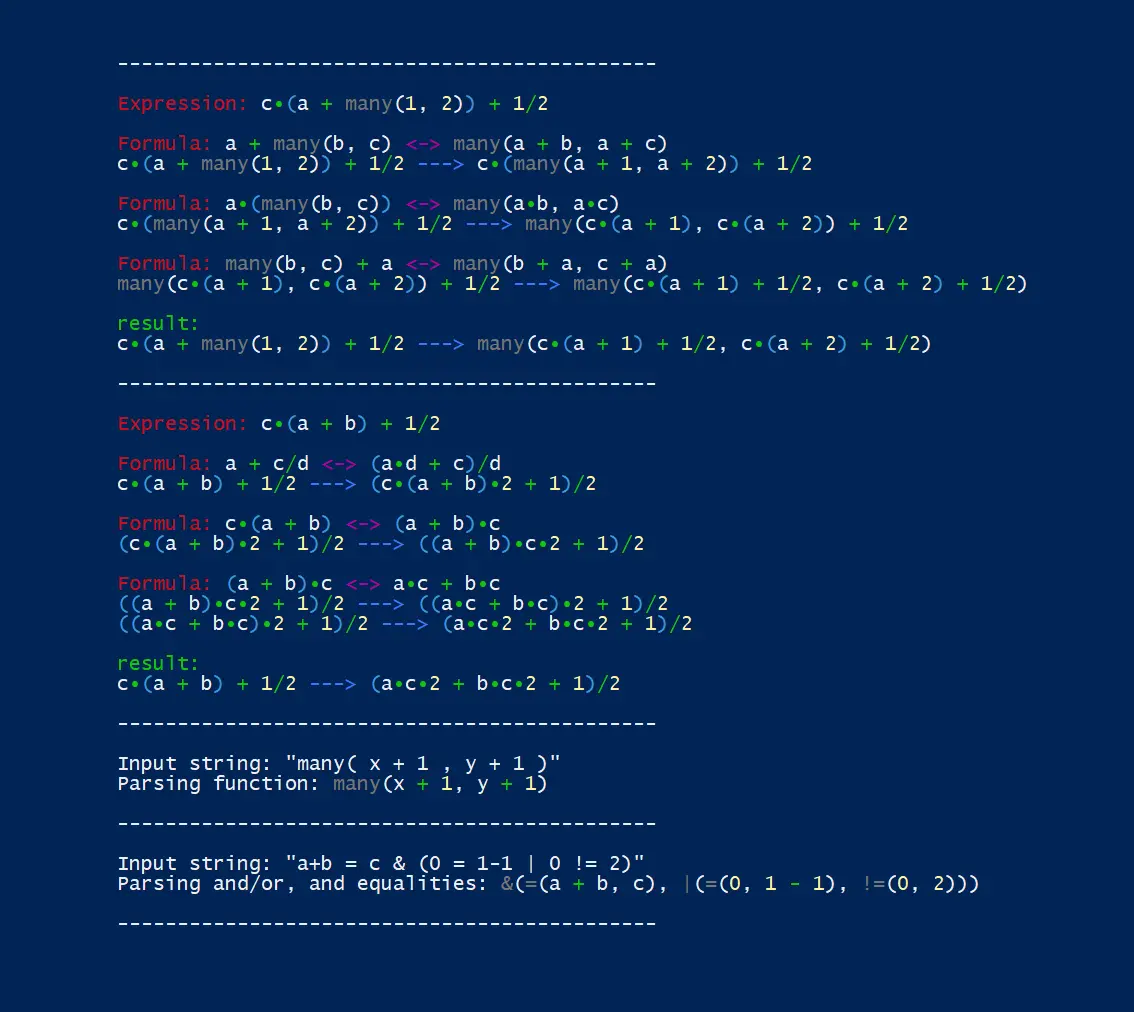
На скриншоте выше:
- Вынесение many из всех функций
- То что было раньше (заметили точку как знак умножения? :) )
- Парсинг функции
- Парсинг логических выражений и неравенств с равенствами.
#17.03.2020
Сейчас разбирался с возможность задания собственного синтаксиса в Sublime text. Если кто будет захочет такое же делать, рекомендую эти ресурсы:
- http://ilkinulas.github.io/programming/2016/02/05/sublime-text-syntax-highlighting.html
- https://www.sublimetext.com/docs/3/syntax.html
- https://www.sublimetext.com/docs/3/scope_naming.html
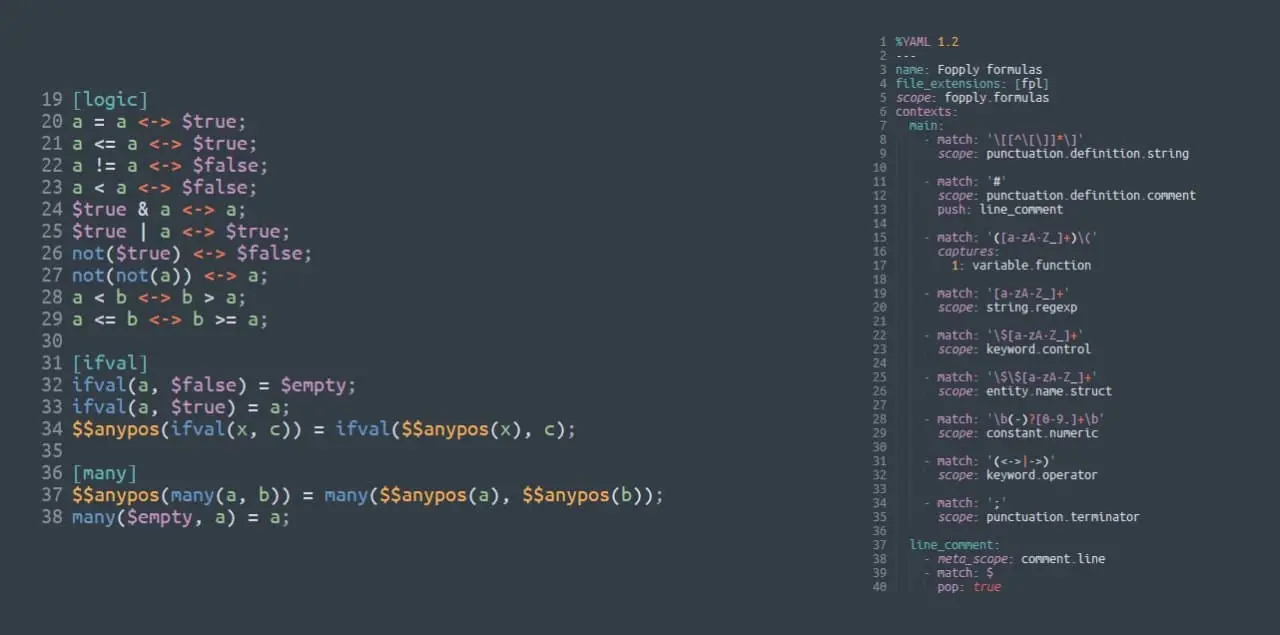
Заставил подсвечивать свои формулы в файлике, потому что впредь планирую читать формулы из файлика, и размышлять там же. Так же параллельно раздумываю над новыми фичами, а именно **встроенными функциями.**Посмотрите на скриншот в следующем сообщении.
Далее я буду использовать термин "паттерн сматчился", что означает тоже самое, что "формулу можно применить". Только я теперь формулу называю паттерном.
Для начала об этих долларах на скриншоте. Доллар перед названием переменной обозначает, что когда формула будет применяться, переменная должна иметь именно это название. То есть "a" - это паттерн в формуле "a+b". А "$true" в формуле "true & a" - это конкретная переменная с именем true.
С функциями всё наоборот. В них изначально "sin(x)" означает, что функция имеет конкретное имя. Если мы хотим написать формулу для любой функции, то нам нужны хаки, а именно доллар. Таким образом: "$f(a, b)" сматчится с любой функцией от двух аргументов, будь то "a+b" или "atan2(y, x)".
Ещё имеются функции с двумя долларами, именно они и будут обозначать что-то встроенное. Например, функция "$$anypos(x)" сматчится с любой функцией с любым количеством переменных, но при этом только если хотя бы один аргумент матчится с паттерном x. Тогда этот паттерн берётся, и производится преобразование над этой функцией только внутри этого аргумента. Лучше покажу на примере. Пусть имеется такая формула:
$$anypos(many(a, b)) = many($$anypos(a), $$anypos(b));
Тогда по этой формуле:
myfunc(many(a, b), y, z) = many(myfunc(a, y, z), myfunc(b, y, z))
В данном случае myfunc сматчилась с $$anypos, а первый её аргумент с many(..), и при использовании формулы все остальные аргументы функции myfunc остались неизменны.
Так же думаю что должна быть встроенная функция, которая арифметические выражения, и должны быть матчинги типов через два доллара, например, $$n должен матчиться с любым числом.
Как видно, я хочу всю логику оперирования математикой вынести в формулы и свой язык, а в коде держать всё максимально абстрагированно от математики. Мне кажется этот подход хорош тем, что на моём языке можно будет описать, например, общую алгебру. И он будет безопаснее, чем кодировать это в коде, но при этом будет работать долго.
Надо ещё подумать как записывать вывод формул из одних в другие.
jpg
#22.03.2020
Итак, мне на курсовую работу дали задание переписать прошлогоднюю курсовую на другие базисные функции. У меня были линейные, а надо заюзать квадратичные.
Проблема в том что в учебники, где описана вся теория, имеются матрицы для линейных функций, а для квадратичных описано словами как их получать. Ну и чтобы их получить, необходимо взять много интегралов.
Как уже стало понятно из моей автоматизации кликания мышкой в программе, я очень не люблю работать ручками, поэтому я написал прогу на питоне, которая использует sympy для того чтобы брать эти интегралы.
В общем она брала интегралы для 81 элемента матрицы, и делала это очень долго, и на следующей картинке я покажу результат.
Пока я это делал, я понял что sympy слаб, в нём нельзя:
- Разделить матрицу с суммами внутри на сумму матриц
- Вынести из матрицы общий множитель
Приходится это делать костылями в виде умножения и упрощения на обратное значение, которое я сам задал, или в виде сохранения элементов в кишках вычислений в разные матрицы.
Если вы знаете какие-то нормальные библиотеки для работы с символьными вычислениями, или программы которые позволяют интерактивно взаимодействовать, то поделитесь пожалуйста.
А пока я такие библиотеки или программы не знаю, постепенно двигаюсь к созданию своей, которую описывал в предыдущих постах (fopply).
А вообще я не представляю как такие вычисления делать на бумажке, это же бред! Вообще я считаю что в университете или даже в школе параллельно с курсом математики должны учить решать все задачи на условном sympy.
А если у меня есть подписчики, которым в жизни предстоит ещё много работать с матаном, изучайте sympy! Упростите себе жизнь, пишите калькуляторы для разных действий. Вот, например, у меня на одном предмете были калькуляторы для подсчёта каких-то специальных вещей: @optozorax/math_modeling_controllable_systems
А вот код вычисления этих матриц, кому интересно:
integrate_fem_3.py link
from sympy import *
import copy
a, b, c = symbols("a b c")
x, y = symbols("x y")
def get_function(list, var, xy, h):
a1 = solve([
a*xy*xy + b*xy + c - list[0],
a*(xy + h/2)*(xy + h/2) + b*(xy + h/2) + c - list[1],
a*(xy + h)*(xy + h) + b*(xy + h) + c - list[2]
], (a, b, c))
return a1[a]*var*var + a1[b]*var + a1[c]
x_p, h_x = symbols("x_p h_x")
x_p1 = x_p + h_x
y_p, h_y = symbols("y_p h_y")
y_p1 = y_p + h_y
X1 = get_function([1, 0, 0], x, x_p, h_x)
X2 = get_function([0, 1, 0], x, x_p, h_x)
X3 = get_function([0, 0, 1], x, x_p, h_x)
Y1 = get_function([1, 0, 0], y, y_p, h_y)
Y2 = get_function([0, 1, 0], y, y_p, h_y)
Y3 = get_function([0, 0, 1], y, y_p, h_y)
f = []
for i in [Y1, Y2, Y3]:
for j in [X1, X2, X3]:
f.append(j*i)
G1 = zeros(len(f))
G2 = zeros(len(f))
for i, a in enumerate(f):
for j, b in enumerate(f):
temp = simplify(
integrate(
integrate(
diff(a, x) * diff(b, x) + diff(a, y) * diff(b, y),
(y, y_p, y_p + h_y)
),
(x, x_p, x_p + h_x)
)
)
(first, second) = temp.args
(coef, up, down) = first.args
if up == h_x:
G1[i, j], G2[i, j] = first, second
else:
G1[i, j], G2[i, j] = second, first
M = zeros(len(f))
for i, a in enumerate(f):
for j, b in enumerate(f):
M[i, j] = simplify(
integrate(
integrate(
a * b,
(y, y_p, y_p + h_y)
),
(x, x_p, x_p + h_x)
)
)
first = h_x/(h_y*6*15)
second = h_y/(h_x*6*15)
G1 = simplify(G1 / first)
G2 = simplify(G2 / second)
l = Symbol("lambda")
print("G = {}\\cdot{} + {}\\cdot{}".format(latex(l * first), latex(G1), latex(l * second), latex(G2)))
multiplier = h_x*h_y/36/25
M = simplify(M / multiplier)
g = Symbol("gamma")
print("M = {}\\cdot{}".format(latex(g * multiplier), latex(M)))

jpg
Чтож, я закончил эту работу, ветка замержена. Рассказывать больше особо нечего, потому что тут слишком много контекста. Да и я просто переделал прошлогоднюю работу на немного другое основание.
Так что просто полюбуйтесь какие божественные автогенерируемые отчёты в LaTeX с королевскими исследованиями я раньше делал: link to pdf.

jpg
#1.07.2020
Я только что осознал что придуманные там функции, которые обладают свойством "выходить из любой другой функции" ifval и many, на самом деле противоречат сами себе.
Напомню, что функцию модуля в этих терминах можно описать следующим образом:
abs(x) = many(ifval(x, x >= 0), ifval(-x, x < 0))
И вот с заданными мною свойствами этих функций можно прийти к тому что abs(x) всегда является пустым множеством.

jpg
Вот так можно превратить модуль в пустое множество. Так что придуманные мною обозначения для задания кусочно-заданных функций, вроде модуля, деления на ноль итд, не подходят. И надо искать другие методы формализации кусочно-заданных функций и каким образом мы имеем право преобразовывать такие кусочно-заданные функции в системы уравнений без кусочно-заданных функций.
В школе мы об этом не думаем, а просто следуем 100500 правилам, схожим с правилами бизнес-логики, поэтому когда дело доходит до формализации или попытки написать программу, сталкиваемся с такими трудностями. Возможно, школьную алгебру уже давно формализовали, и все эти трудности там решены, мне просто нужно нагуглить.
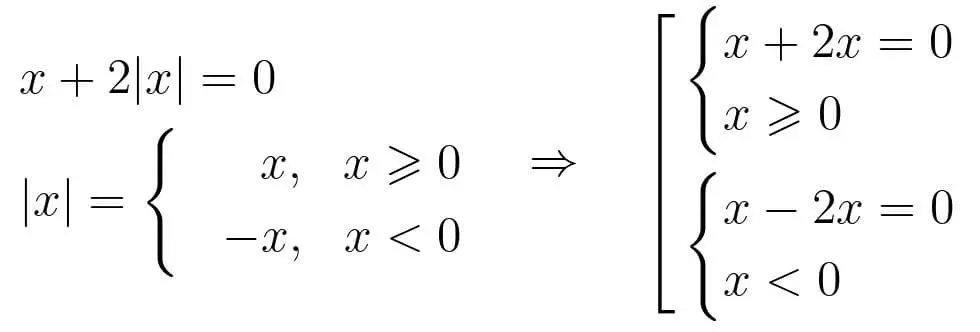
jpg
Мне интересно по каким именно правилам математики мы можем вот так вот взять и вытащить условия модуля за пределы самого модуля, на уровень равенства, где границы этого протаскивания.
#26.08.2020

jpg
А ещё я наконец решил "фундаментальные проблемы математики", которые описывал в ранее.
Повторю суть: я хочу написать программу для символьных (аналитических) вычислений. Хочу чтобы там можно было выводить формулы из аксиом и других формул. Для этого мне нужно записать аксиомы над стандартными операциями и функциями. Всякие коммутативности/ассоциативности для сложения-деления-умножения я легко записал. Проблемы начались когда мне надо было придумать представление для частично заданных функций, например: модуль, знак. Как задавать такие функции, чтобы над ними можно было совершать операции, и как записать аксиомами их структуру?
Я придумал такие операторы как ifval и many, которые подробно описаны в /99. Я надеялся комбинацией этих операторов записать частично заданную функцию. В итоге оказалось, что эти операторы настолько широкие, что они приводят к противоречиям, и на практике их использовать невозможно.
После этого я встрял в разработке, я не мог двигаться дальше из-за этой проблемы, потому что она находится в самой основе. Я пытался придумать односторонние формулы, думал над типизацией, ничего не помогало.
Но вот недавно, после релиза репозитория с эволюцией, я сел за fopply, немного подумал, и нашёл решение!
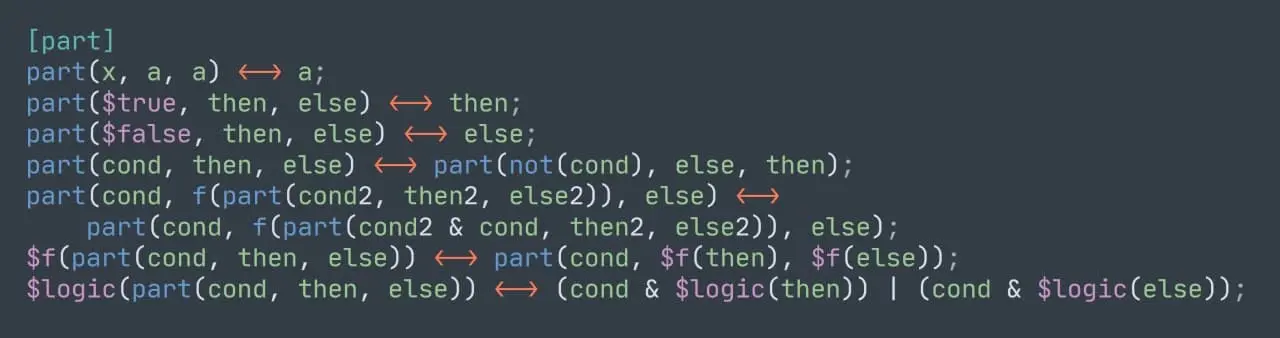
Надо ввести одну функцию для этого дела: part(cond, then, else). То есть эта функция возвращает then, если в cond находится $true, либо else иначе.
jpg
Напоминаю что формулами можно пользоваться как в прямую сторону, так и в обратную. Здесь я записал базовые свойства над этой функцией и как её можно превратить в логические операторы.
Правда последняя формула уже требует от меня реализации типизации с разделением на число и логическое значение, иначе оно не будет иметь смысла, если превратить модуль в логическую структуру посередине обычной формулы.
С помощью этой функции я смог записать модуль, sign, и даже смог из базовых формул вывести эту: a <-> part(b == 0, a, a*b/b) (к формуле можно добавить умножение чего-то на самого себя, если это что-то не равно нулю). А раз я смог формально вывести такую экзотику, значит я иду по правильному пути.
Так же я избавился от такой концепции как anypos, принцип которой описан в /101. Я пытался в структуре формулы записать что она способна быть в любом аргументе функции. То есть если записано: $$anypos(x+1), то оно может сматчиться с функцией f(y-2, z+3, 2+1) в третьем аргументе. Затем выдумывал множество способов записать когда этих аргументов два, как записать перестановки итд. Но потом понял что подготавливать выражение к такому виду чтобы оно смогло сматчиться с формулой - дело пользователя. То есть, если у пользователя есть функция: f(y-2, z+3, 2+1), то он делает замену g(x) := f(y-2, z+3, x), и затем записывает g(2+1), которая уже легко сматчится с формулой, работающей над формулами с одним аргументом. Таким же образом можно заставить работать формулы глубоко внутри, а не только в каком-то аргументе. Благодаря этому основа программы очень сильно упростится.
В общем, чувствую, я наконец могу начать писать код и получать свой дофамин.
#6.09.2020
А тем временем у меня большой апдейт по fopply!!!
Для начала дизайнерские штуки.
#2Биндинг.
Предположим, у нас есть формула: part(x, a, a) <-> a и есть выражение x+1, я хочу применить эту формулу справа-налево, тогда чем у меня должен быть x из формулы? По идее там должно быть что угодно, ведь если я применяю слева-направо, то информация о x тупо стирается.
Я придумал что можно вручную записать чему будут равны неизвестные переменные формулы следующим образом: x := x = 0 (это я называю биндингом), тогда результат будет: part(x = 0, x+1, x+1). У формулы и выражения собственное пространство имён, так что коллизий с иксом с одной стороны и с другой не возникает.
#2Задание положения
Например, у нас есть формула a+b <-> b+a и есть выражение 2*(3+4). Как мне применить эту формулу внутрь выражения? Можно вручную записать позицию в виде массива: [1], и применять формулу к внутренней части. Но это неудобно для пользователя, поэтому я придумал следующую запись:
2*(3+4)
. ^^^
При парсинге будет сохранена вся информация о расположении частей формулы, и мы сможем восстановить позицию в виде массива по такой записи. Точка вначале нужна, потому что мне пока лень парсить отступы, и она нужна чтобы указать начало.
Хотя вчера друг предложил мне что можно прямо внутри формулы записывать задание позиции, например так: 2+({3+4}).
Замечание: нельзя записать:
1+2+3+4
. ^^^
потому что формула представляется деревом следующего вида: +(1, +(2, +(3, 4))). Соответственно не существует такого под-дерева в этом дереве, которое было бы равно +(2, 3). Здесь нужно только преобразовывать исходное выражение.
#2Матчинг произвольной функции
Итак, у нас есть формула: a = b & $f(a) <-> a = b & $f(b). Эта формула означает, что если у нас где-то записано a = b, то мы можем в местах, где это равенство записано через логический оператор И, заменить переменную a на переменную b. $f(a) здесь означает "любая функция с одним аргументом, который матчится в паттерн a".
То есть данная формула может быть применена к:
1. a = 1 & a
2. a = 1 & c+a = 0
3. a = 1 & (x*a + b*a + a*a = 0 | x = 5)
Первый случай тривиальный. А что делать со вторым и третьим? Как нам найти то самое место что матчится с a? Первое что приходит на ум - это брать известную нам информацию с чем оно должно матчиться и рекурсивно пройтись и произвести замену.
С первыми двумя этот подход сработает, но проблемы начнутся на третьем. Мы должны сматчить первое совпадение? Второе? Третье? А если я хочу заменить на единицу только второе и третье с четвёртым совпадение с a, а первое в x*a оставить?
И вот для таких случаев я придумал, что нужно вручную записать паттерн, который будет считаться $f, например: $f(x) := a + b*x + x*x | c для третьего случая.
В данном случае сматчится следующим образом:
a := x*a
b := b
c := x = 5
Заметьте, что в этом паттерне можно описать только структуру, не надо описывать один в один всё выражение.
Для формулы $f(sin(a)) и выражения sin(1+2) * sin(1+2) можно записать паттерн $f(x) := x * x, в итоге оно сматчится с x := sin(a), а затем a сматчится с 1+2.
Конечно, в будущем для этого будет сделан интерфейс, чтобы такое можно было натыкать мышкой.
#2Аксиомы и доказательства
Следующее что я придумал - это что должны быть формулы которые записываются как аксиомы, и формулы, которые выводятся из других, и это можно доказать.
Для такой системы все формулы должны быть записаны в каком-то файле, с именами и номерами, чтобы на них можно было ссылаться и использоваться в выводе или "доказательстве".
Именно такое я и сделал в этом файле: math.fpl. Весь сложный синтаксис я уже описал ранее, оставшийся синтаксис в этом файле интуитивно понятен.
Кстати, я там заложил на будущее формулу unsafe, которая имеет следующий вид: a <-> b, то есть с помощью неё можно заменить что угодно на что угодно 😄
В этом файле я записал базовые формулы и даже доказательства, использовал всё что рассказал ранее. Поэтому теперь главной задачей стоит: запрогать считывание этого файла во внутреннюю структуру и проверку доказательств.
#2Успехи в программировании
И я сделал эту проверку и всё что описано выше, всё работает! 🎉🎉🎉
Можно зайти в репозиторий, модифицировать fpl/math.fpl, писать свои аксиомы, свои доказательства, и запускать проверку доказательств через cargo run.
В плане кода там пока что неоптимальный говнокод, ибо я стараюсь экономить время, всё сделано чтобы просто работать. Доказательство проверяется, и если в каком-то шаге специально сделать ошибку, программа об этом скажет, но без места где эта ошибка возникла. Поэтому пожалуйста, если знаете, поскидывайте в только что созданный чат у данного канала, статей как архитектурно организовать вывод ошибок для своего языка.
А следующей проблемой, с которой предстоит разобраться - это как работать с числами внутри формул, чтобы можно было записать что подобные можно приводить, что числа можно сокращать и умножать, а ещё делать это в обратную сторону.
А, ну и раз я поступил в магистратуру, надо бы найти преподавателя, который согласится взять эту тему на магистерскую диссертацию. Надеюсь найду, а то я не хочу тратить своё время на какую-нибудь фигню.
#31.01.2021
А я вспомнил, что существует #fopply! Я немного посидел над ним и приделал нормальные сообщения об ошибках. Для этого пришлось немного подредачить парсер и написать тонну кода обработки ошибок. В будущем для этого планирую заюзать библиотеку codespan.
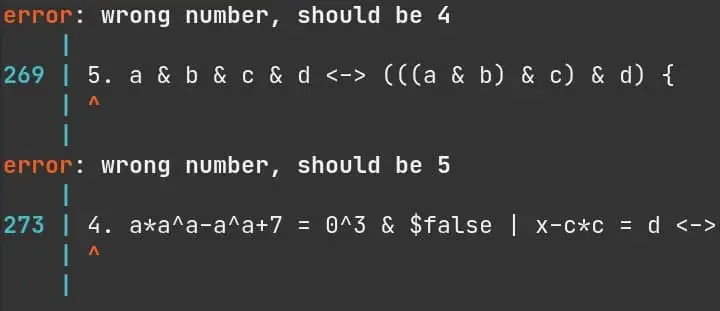
У меня выводится сразу несколько сообщений об ошибках, которые можно получить на текущем этапе проверки. Некоторые самописные ЯП'ы таким похвастаться не могут!
Чтобы получить сообщения об ошибках, которые указывают на место ошибки, пришлось сделать такую структурку:
struct Spanned<T> {
span: Range<usize>,
inner: T,
}
И обернуть в эту структурку множество всяких полей других структур, которые образуют формулу и доказательство.
Так же через новую версию, благодаря сообщениям об ошибках, которые указывают на проблему, я смог доказать (a+b)*(a-b) = a*a-b*b.
Следующим этапом планирую написать интерактивное приложение, в котором можно интерактивно применять формулы, находить все возжможные формулы, которые подходят к текущему выражению. Далее я собираюсь через него начать заносить как можно больше известных мне формул, чтобы найти проблемные места и лучше понять как их разрешить в будущем.
А вот так теперь выглядят сообщения об ошибках в fopply:
jpg
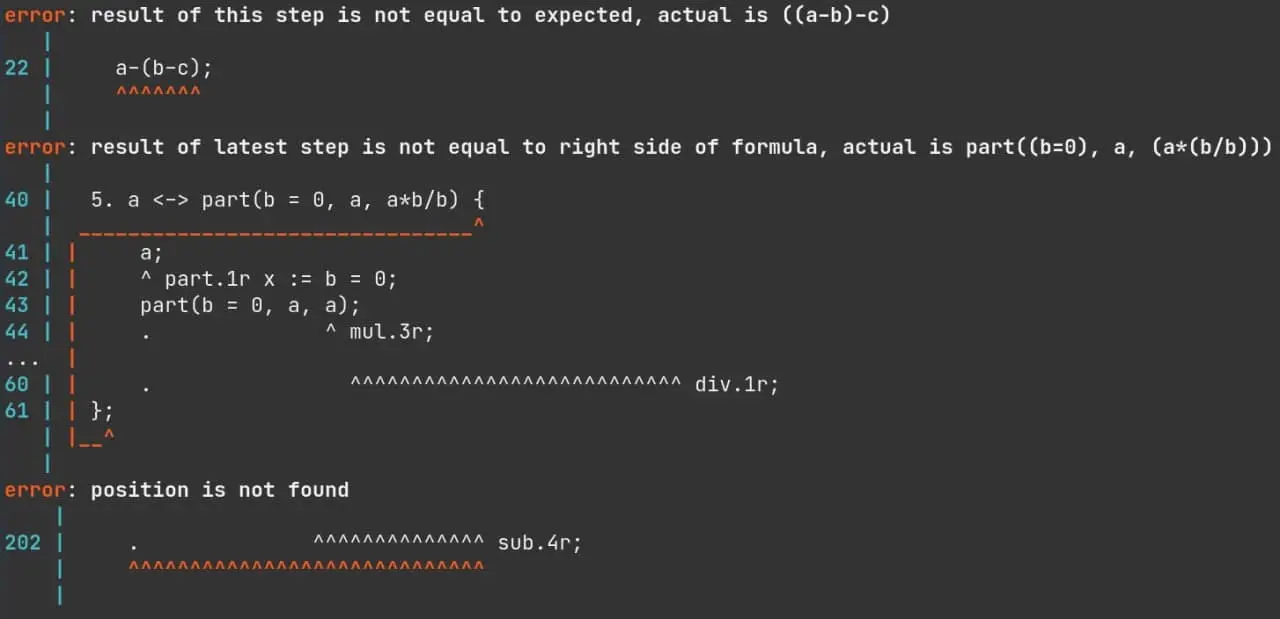
jpg
#27.03.2021
Источник:
tg/391(9 💬).
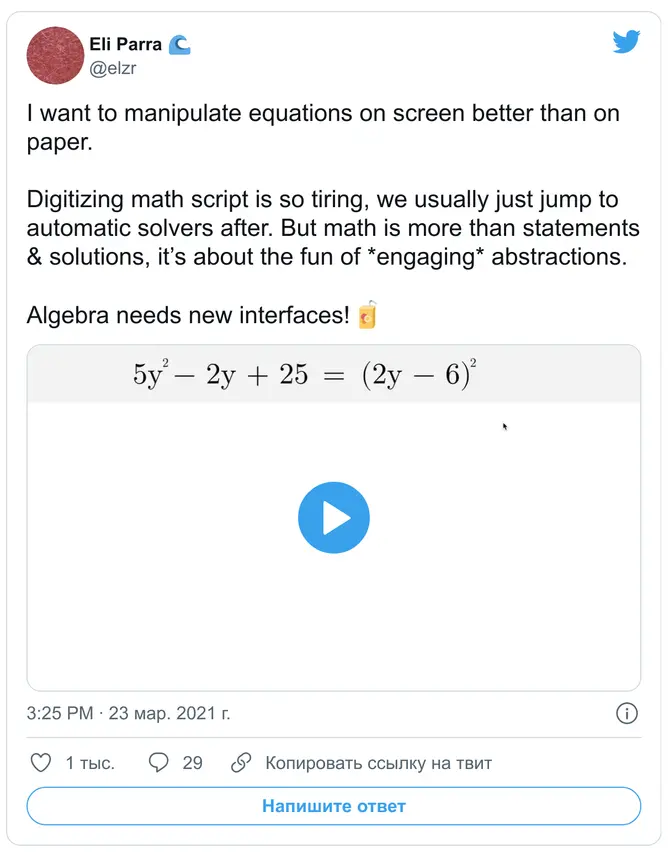
Недавно в твиттере увидел эту шикарную анимацию об идее интересного интерфейса для алгебры. На примере этой анимации можно увидеть ту степень пошаговости, которую я хочу для fopply. Правда у него в анимации интерфейс сильно оптимизирован под работу с базовой алгеброй, например при взятии степени и перетаскивании её на другую сторону равенства, она превращается в квадратный корень. Это, наверное, уже оверкилл, но выглядит прикольно.
Так же он говорит что было бы очень круто увидеть что получится, если младенцы будут играться с такой программой, что если они выработают интуицию и ощущеные красоты в математике ещё в таком раннем возрасте? Получится ли ещё один Рамануджан? Мне тоже очень интересно такое применение формальных пошаговых алгебраических систем. У меня была идея по представлению какой-нибудь тригонометрии не в виде формул, а в виде геометрических структур с 3D, и чтобы операции над структурами просто являлись тригонометрическими формулами. Будет ли на этой основе игра интересна людям, и в частности детям? Получится ли научить их любить математику через такие игры? 🤔
png
