#Введение
Недавно я разработал и опубликовал библиотеку под названием Space Objects. Это библиотека для работы с векторами, прямыми, плоскостями; она реализует преобразования координат; нахождения пересечений этих объектов и т. д. Эта библиотека выросла из моего другого проекта.
После того, как я её опубликовал и начал придумывать примеры использования, я осознал всю её мощь. Она является апогеем множества проектов, которыми я ранее занимался: 2D графика, фракталы, рендеринг 3D. Всё это в кратком виде имеется в примерах этой библиотеки на GitHub.
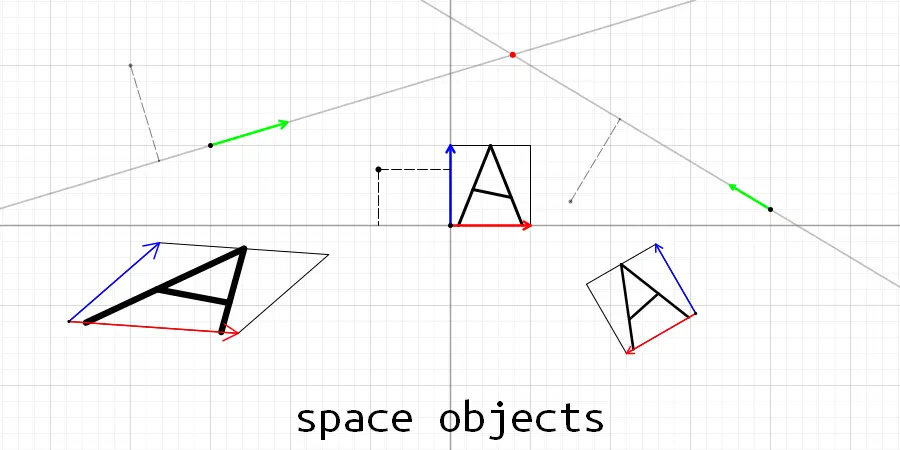
Лого библиотеки, на ней показаны все основные объекты и действия для двумерного пространства.
png
Я расскажу об особенностях этой библиотеки на основе задачи рисования фрактала дерево Пифагора.
А для начала немного изучим логотип библиотеки. Здесь стандартной системой координат изображается та система, что находится в центре. Другие системы координат показаны без сетки, только с положением центра и направляющими векторами.
Как можно увидеть, система координат может быть не только смещена относительно стандартной в любое место, но ещё наклонена, и повернута на любой угол, она даже может быть зеркально отраженной.
Для каждой системы координат рисуется квадрат с координатами (0, 0), (0, 1), (1, 1), (1, 0), а так же буква A, чтобы показать возможность преобразования координат. Если говорить подробнее, то прежде чем нарисовать квадрат, его координаты преобразуются по текущей системе координат при помощи функции from() ("из" системы координат), и только преобразованные координаты рисуются отрезком.
#Рисуем дерево Пифагора
#2Как его строить
Пусть у нас есть начальные координаты самого первого квадрата. Далее, согласно определению этого фрактала, надо построить на его верхней стороне прямоугольный треугольник с координатами, затем же надо получить оба катета этого прямоугольного треугольника и рекурсивно проделать тоже самое на них.
Наглядно этот процесс можно увидеть на следующей гифке.
Самое сложное в рисовании этого фрактала - вычисления координат каждого квадрата.
Так же, очевидно, для рисования дерева Пифагора необходимо использовать рекурсию. И нам необходимо написать такую рекурсивную процедуру, которая будет строить дерево Пифагора на основании любого отрезка. Ведь каждая новая его часть все-же строится на основании стороны треугольника, то есть отрезка с произвольными координатами.
#2Сложный и плохой путь
Когда я в 10 классе, ещё программируя на Паскале, задался задачей нарисовать этот фрактал, я пошел самым сложным путем, вычисляя громоздкие формулы, с использованием геометрии и тригонометрии. В итоге у меня вышел такой код:
var alpha:real; // Угол при основании прямоугольного треугольника
procedure recur(x,y, x1,y1:real; g:integer);
var dx,dy,lx,ly:real;
x2,y2,x3,y3:real;
begin
if (g=1) or ((sqr(x-x1)+sqr(y-y1))<1) then
// Выходим из рекурсии, если достигнута максимальная глубина или
// размер квадрата слишком мал
else
begin
{1)}dx:=x1-x;
dy:=y1-y;
{2)}x2:=x-dy; // Вычисляем две другие точки квадрата по имеющимся
y2:=y+dx; // точкам x,y, x1,y1.
x3:=x1-dy;
y3:=y1+dx;
{3)}draw_Rect(x,y, x1,y1, x2,y2, x3,y3); // Рисуем квадрат на экран
// Вычисляем координаты вершины прямоугольного треугольника
{4)}lx:=sin(2*alpha)/2*dy-sqr(cos(alpha))*dx;
ly:=sqr(cos(alpha))*dy+sin(2*alpha)/2*dx;
// Вызываем рекурсию для каждого катета прямоугольного треугольника
{5)}recur(x2,y2, x2-lx,y2+ly, g-1);
recur(x2-lx,y2+ly, x3,y3, g-1);
end;
end;
Если необходимо понять каждое действия, есть комментарии, да и вообще код довольно простой, даже если вы не знаете Паскаль, вы его наверняка поймете. Но разбираться в нём не нужно, он лишь служит демонстрацией сложного подхода.
В функцию recur передаются координаты двух точек, на основе отрезка, на основании отрезка, образованного этими двумя точками, строится квадрат; этот квадрат рисуется; на стороне квадрата, которая параллельна данному отрезку, строится прямоугольный треугольник, и для его катетов вызывается эта же функция.
Минусы этого кода:
- Здесь не используются классы векторов, которые бы позволили сократить часть кода, связанную с суммой по координате x и y, вычисления длины стороны квадрата и сокращения количества передаваемых параметров.
- Весь квадрат задается лишь одной стороной, и далее непонятными формулами вычисляются координаты других его вершин.
- Координаты прямоугольного треугольника на основе квадрата, заданного лишь одной стороной, вычисляются очень сложно, и непонятно как эти формулы работают.
- Код применим только для построения дерева на верхней стороне квадрата, если захочется построить на боковой, или чередовать это, то придется вычислять новые формулы.
- Данное решение применимо только к квадрату. Его нельзя использовать для произвольного многоугольника.
Но, благо, здесь хотя бы можно менять угол при основании прямоугольного треугольника. И в то время я получил примерно следующую анимацию:
#2Путь получше и с использованием библиотеки
Библиотека предоставляет две вещи, которые нам сейчас пригодятся:
- Преобразование вектора из одной системы координат в другую.
- Создание системы координат из двух точек при помощи функции
makeLine2.
makeLine2(a, b) работает следующим образом: создается система координат с центром в точке a, вектор первой оси направлен в сторону b и по длине равен (b-a). Второй вектор оси равен первому, повернутому на 90 градусов против часовой стрелке. То есть такая система координат всегда ортогональна (оси перпендикулярны).
Построение дерева Пифагора будет аналогично предыдущему пункту, только мы будем передавать в функцию не координаты отрезка, на основании которого строить дальше, а систему координат, в которой надо строить дальше.
Так как мы можем легко преобразовывать координаты, то для любой фигуры, будь то квадрат, прямоугольный треугольник или дерево Пифагора, нам надо знать их координаты, когда они одной своей стороной полностью лежат на красной оси X, которая задается вектором i. Такое необходимо, потому что далее мы будем преобразовывать их координаты к некоторой системе, полученной с помощью функции makeLine2, и в итоге преобразованный многоугольник автоматически будет располагаться как бы прикрепленным к какой-то стороне, сразу масштабированный под размер этой стороны.
Получившийся код:
void draw_pythagoras_tree(const space2& space) {
// Выходим из рекурсии, если одна из осей (аналогично и сторона квадрата) имеет длину меньше, чем 2
if (space.i.length() < 2)
return;
// Задаем координаты квадрата
vec2 a(0, 0), b(0, 1), c(1, 1), d(1, 0);
// Высчитываем координаты прямоугольного треугольника, который лежит своей гипотенузой на оси X, с углом alpha при основании
double alpha = spob::deg2rad(10);
vec2 tr_a(0, 0), tr_b(1, 0), tr_c(cos(alpha), 0);
tr_c = rotate(tr_c, vec2(0), alpha);
// Преобразуем квадрат из текущих координат к координатам переданного пространства
a = space.from(a);
b = space.from(b);
c = space.from(c);
d = space.from(d);
// Рисуем квадрат
draw_line(a, b);
draw_line(b, c);
draw_line(c, d);
draw_line(d, a);
// Строим пространство, которое находится на верхней стороне квадрата
space2 tr_line = makeLine2(b, c);
// Переводим координаты треугольника к этому пространству
tr_a = tr_line.from(tr_a);
tr_b = tr_line.from(tr_b);
tr_c = tr_line.from(tr_c);
// Строим пространства, которые находятся на обоих катетах этого треугольника
space2 l1 = makeLine2(tr_a, tr_c);
space2 l2 = makeLine2(tr_c, tr_b);
// Рекурсивно строим дерево в этих пространствах
draw_pythagoras_tree(l1);
draw_pythagoras_tree(l2);
}
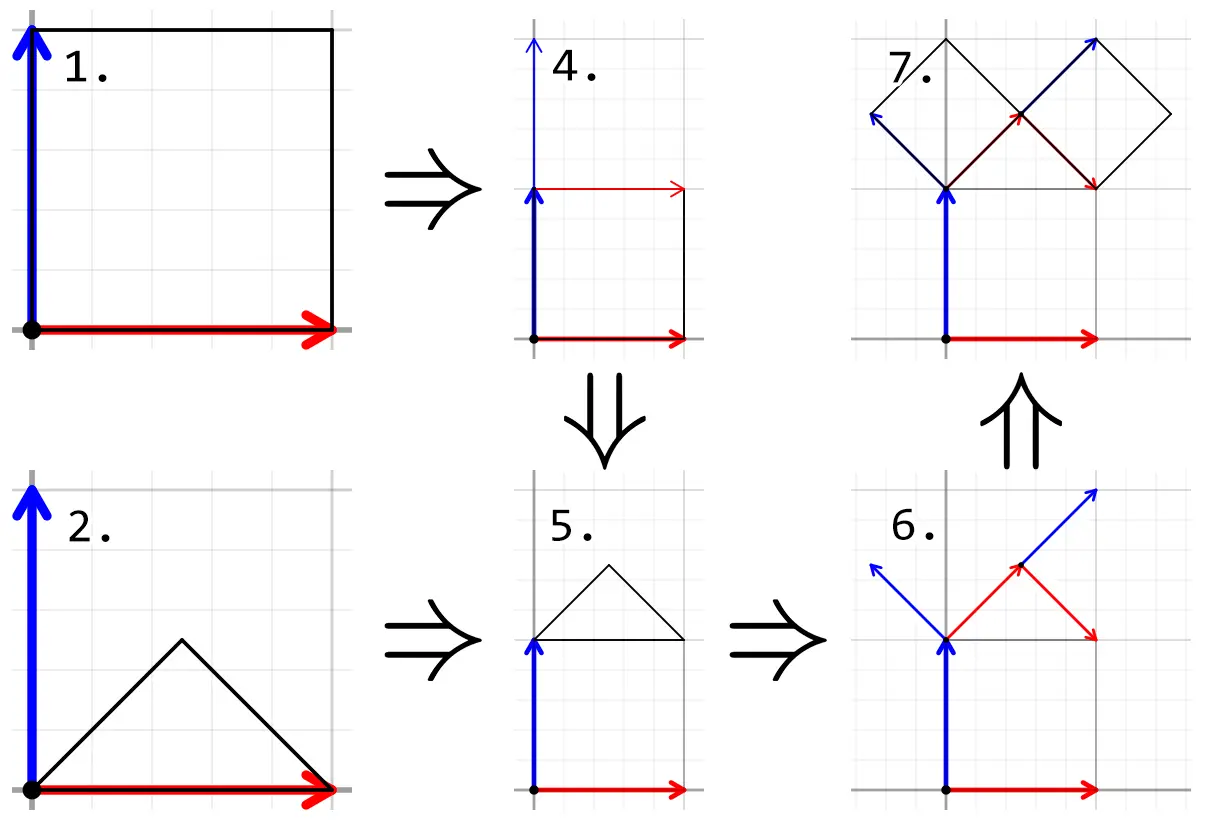
Пошаговое описание действий с визуализацией вычислений:
png
- Создаем координаты квадрата.
vec2 a(0, 0), b(1, 0), c(1, 1), d(0, 1); - Высчитываем координаты прямоугольного треугольника. Здесь никаких сложных формул нет, только простейшая геометрия, и использование функции
rotate(что, вокруг чего, на какой угол).vec2 tr_a(0, 0), tr_b(1, 0), tr_c(cos(alpha), 0); tr_c = rotate(tr_c, vec2(0), alpha); - Видно, что координаты квадрата заданы без привязки к какой-то системе координат, просто нули и единицы. Поэтому переводим его координаты из системы координат, которую нам предоставили в функции.
Заодно сразу же рисуем этот квадрат.a = space.from(a); b = space.from(b); c = space.from(c); d = space.from(d);draw_line(a, b); draw_line(b, c); draw_line(c, d); draw_line(d, a); - Создаем систему координат на верхней стороне квадрата с помощью функции
makeLine2.space2 tr_line = makeLine2(d, c); - Преобразуем координаты треугольника к координатам только что полученной системы координат.
tr_a = tr_line.from(tr_a); tr_b = tr_line.from(tr_b); tr_c = tr_line.from(tr_c); - Строим новые системы координат на каждом катете полученного треугольника.
space2 l1 = makeLine2(triangle[0], triangle[2]); space2 l2 = makeLine2(triangle[2], triangle[1]); - Повторяем всю процедуру рекурсивно для каждой системы координат, предварительно преобразовав её из переданной системы координат. Вообще от этого преобразования можно было бы избавиться, если бы мы изначально преобразовали координаты квадрата, как это сделали с треугольником.
draw_pythagoras_tree(space.from(l1)); draw_pythagoras_tree(space.from(l2));
Если для написания кода, из плохого пункта выше, я убил много времени на расчет формул на бумажке, на поиск багов и подбор параметров, то первичную версию данного решения я написал реально за полчаса, и занимала она, грубо говоря, 7 строк. Следующие версии модифицировались, чтобы быть более понятными для других людей.
- Здесь используются классы векторов и систем координат.
- Координаты квадрата вычисляются интуитивно понятным образом.
- Координаты прямоугольного треугольника вычисляются очень просто.
- Код применим для построения дерева Пифагора на любой стороне квадрата, надо лишь изменить параметры в строке
space2 tr_line = makeLine2(b, c);. - Данное решение можно применить к любому многоугольнику (главное, чтобы он своей стороной полностью лежал на оси Х).
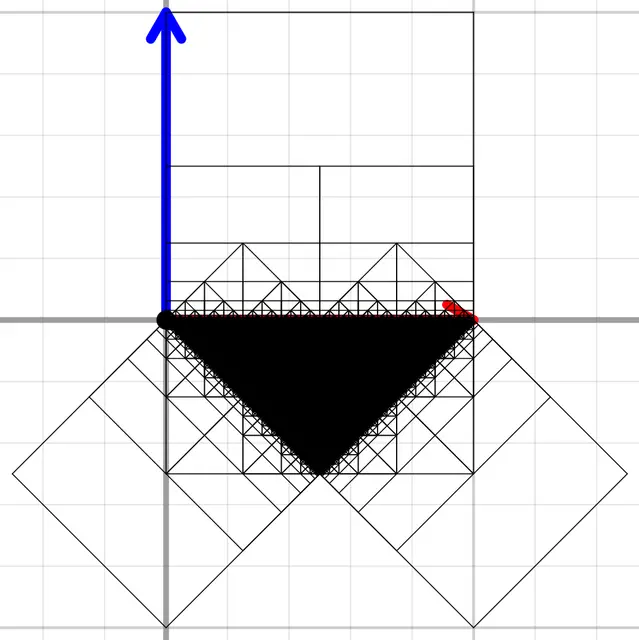
И вот, например построение дерева Пифагора на 0 и 1 стороне квадрата:
space2 tr_line = makeLine2(b, a);
png
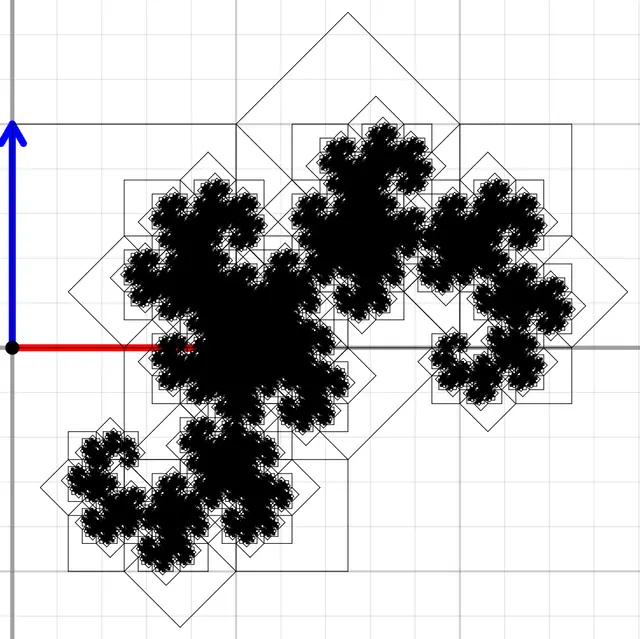
space2 tr_line = makeLine2(a, c);
png
Далее я немного изменил рисование, теперь вместо рисования лишь линий, рисуются многоугольники, в итоге картинка выглядит намного красивей. Так же из-за того, что размеры всё время меняются, я каждый раз вычисляю новые границы, где задано изображение, и смещаю фрактал так, чтобы он полностью помещался в изображении. Вот анимация для каждого дерева Пифагора на основе квадрата:
#Рисуем дерево Пифагора на основе произвольного многоугольника
Как уже упоминалось раннее, хорошее решение можно использовать для любого многоугольника в принципе, с небольшими модификациями. После написания той программы в 10 классе я не остановился, и захотел сделать решение для правильного многоугольника. Так получилось...
#Старое и кошмарное решение
procedure mnogoug(n,m:integer; x,y,x1,y1:real;var x2,y2,x3,y3:real);
{Очень универсальная процедура для построения правильных многоугольников!!!}
{Процедура строит многоугольник с количеством сторон равным n, и причем строится он так,
чтобы основанием была сторона с координатами x,y,x1,y1 , и когда его основание это
данная сторона,то ещё надо вернуть координаты стороны с номером m, в x2,y2,x3,y3 ,
и так как дается только количество сторон и координаты основания,то размер фигуры выбирается
в соответствии с исходными данными, угол наклона,и координаты центра точно так же,причем,
важную роль играет куда положить первую точку, в x,y или в x1,y1 , в зависимости
от этого ваша фигура может быть перевернутой или нет}
var v:integer;
begin
{Находим координаты центра}
rx:=(x1+x)/2+((cos(pi/n)/sin(pi/n))*(y1-y))/2;
ry:=(y1+y)/2-(cos(pi/n)/sin(pi/n)*(x1-x))/2;
{Находим угол наклона многоугольника}
if (y1=y) or (x1=x) then fi:=pi/n
else fi:=-arctan((x1-x)/(y1-y))+pi/n;
if (y1>y) then fi:=fi+pi;
if y1=y then
if x1>x then fi:=fi+pi/2
else fi:=fi+3*pi/2
else;
{Находим радиус многоугольника}
r:=sqrt(sqr(x1-x)+sqr(y1-y))/(2*sin(pi/n));
{Строим все стороны по очереди}
for v:=0 to n do
begin
{Формулы для нахождения координат точек вершин многоугольника, чтобы
их найти надо знать координаты центра, радиус,и угол наклона, но так
как мы их нашли,то можно спокойно строить многоугольник, формула взята
с Википедии}
xi:=rx+r*cos(fi+2*v*pi/n);
yi:=ry+r*sin(fi+2*v*pi/n);
{Если мы дошли до нужной нам стороны, то возвращаем
её координаты}
if (v=m) then
begin
x2:=xb; y2:=yb;
x3:=xi; y3:=yi;
end
else;
{Рисуем линию одной стороны мнгоугольника}
if v<>0 then
begin
//line(trunc(xb),round(yb),trunc(xi),trunc(yi));
line_m(trunc(xb),round(yb),trunc(xi),trunc(yi));
end;
xb:=xi; yb:=yi;
end;
end;
var i,j:integer;
alpha:real;
procedure recur(x,y,x1,y1:real; g:integer);
{Процедура строит на стороне x,y,x1,y1 многоугольник, с количеством сторон i ,
и в этом многоугольнике на стороне j строит прямоугольный треугольник с углом alpha
,а на его катетах всё повторяется сначал, и так в итоге строится фрактал под названием
"Дерево Пифагора", и не обычное, квадратное, а на основании любого многоугольника}
var
lx,ly:real; x2,y2,x3,y3:real;
begin
if (g=0) or ((sqr(x-x1)+sqr(y-y1))<0.1) then
{Когда радиус многоугольника уже меньше единицы, то строить дальше не стоит,
и когда превышен лимит допустимой глубины}
else
begin
{Строим многоугольник с данным основанием, и данным количеством сторон}
mnogoug(i,j,x,y,x1,y1,x3,y3,x2,y2);
{Так как мы нашли искомую сторону, то на ней находим вершину
прямоугольного треугольника, гипотенузой которого является сторона
которую мыы нашли в прошлом действии, и причем угол при основании
этого треугольника равен alpha}
{1)}dx:=x3-x2;
dy:=y3-y2;
{4)}lx:=sin(2*alpha)/2*dy-sqr(cos(alpha))*dx;
ly:=sqr(cos(alpha))*dy+sin(2*alpha)/2*dx;
{А теперь на катетах этого прямоугольного треугольника и строим
новые многоугольники, а на них опять треугольники ... это и называется
фрактал "Дерево Пифагора"}
{5)}recur(x2-lx,y2+ly,x2,y2,g-1);
recur(x3,y3,x2-lx,y2+ly,g-1);
end;
end;
Вообще, мне страшно смотреть на этот код и вспоминать как я с ним возился... Я старался привести его к красивому виду как мог, но его суть остается в костылях и фиговых решениях. И данная картинка прекрасно его описывает:

jpg
Но я постараюсь это всё изложить, чтобы вы прочувствовали весь ужас.
Главной проблемой в этом коде была часть с вычислением угла в функции mnogoug. Там много разных ифов, которые стоят черт знает зачем, и работают черт знает как. Вообще те строки с углом, были найдены эмпирическим путем, методом тыка. Именно на этой части, в процессе метода тыка, я убил n часов при дебаге.
А потом, в процессе изучения языка C я узнал что существует, посланная с небес, функция atan2... Да, в тех строках написана моя костыльно-велосипедная реализация atan2. Это стало настоящим откровением! Обязательно почитайте об этой функции и используйте её!
А так же я понял, что тот код мог бы написать намного проще, без танцев с бубном, если бы с самого начала выводил эти формулы с углом строго по математике.
А теперь, что же здесь делается? Да всё по сути написано в комментариях. Главная идея в том, что для генерации правильного многоугольника есть формула, взятая с Википедии:
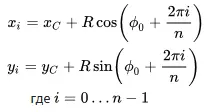
png
Если изучить её, то можно понять, что у правильного многоугольника есть несколько параметров, которые определяют его однозначно: координаты центра C, радиус R и угол поворота ф. И можно вычислить эти параметры, зная n, и координаты одной стороны.
Я выводил формулы для этого на бумажке, и заняло у меня это значительно больше времени, чем просто вывод формул для дерева Пифагора. Именно эти формулы можно видеть в функции mnogoug до цикла. Далее применяется эта формула, чтобы найти координаты стороны многоугольника, на которой будет строиться следующая итерация. Там же сразу рисуются все стороны.
Если смотреть на функцию recur, то там мало чего изменилось, даже формулы для вычисления координат треугольника остались те же.
Ну вот и результаты тех страданий:
Пояснение: тип 20_3 означает, что берется 20-угольник и на его третьей стороне строится остальной фрактал.
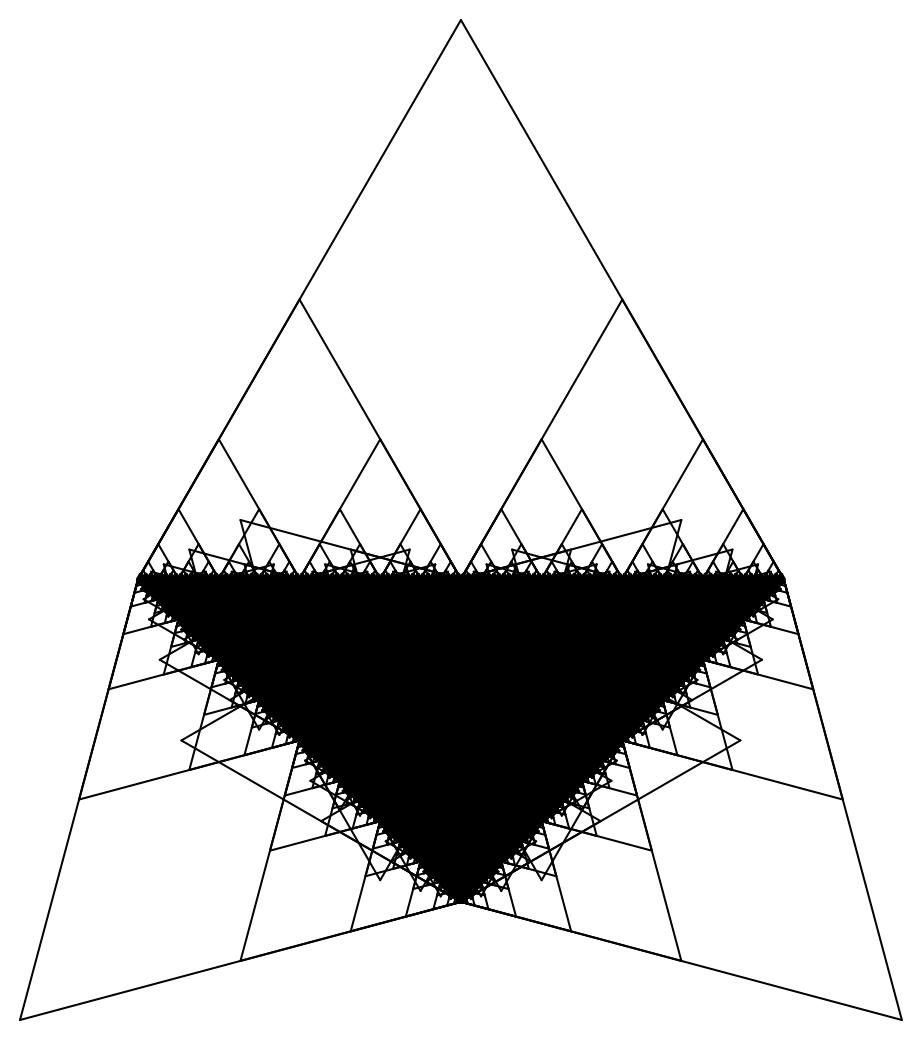
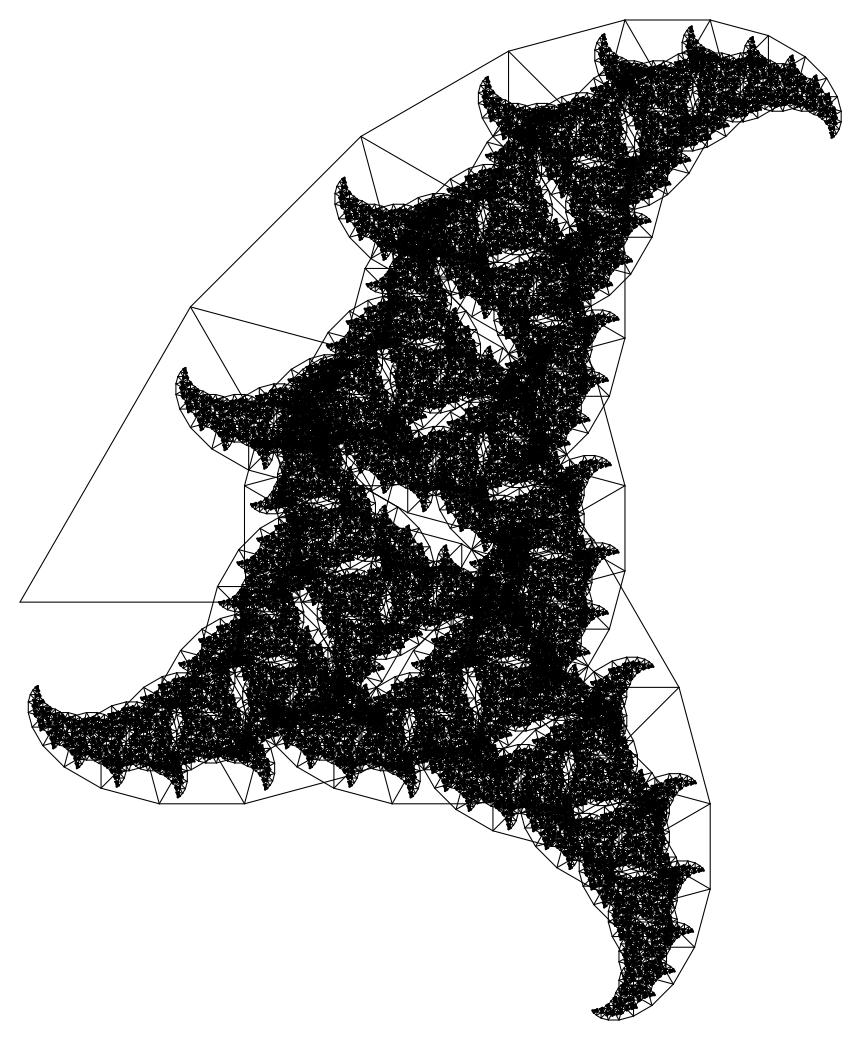
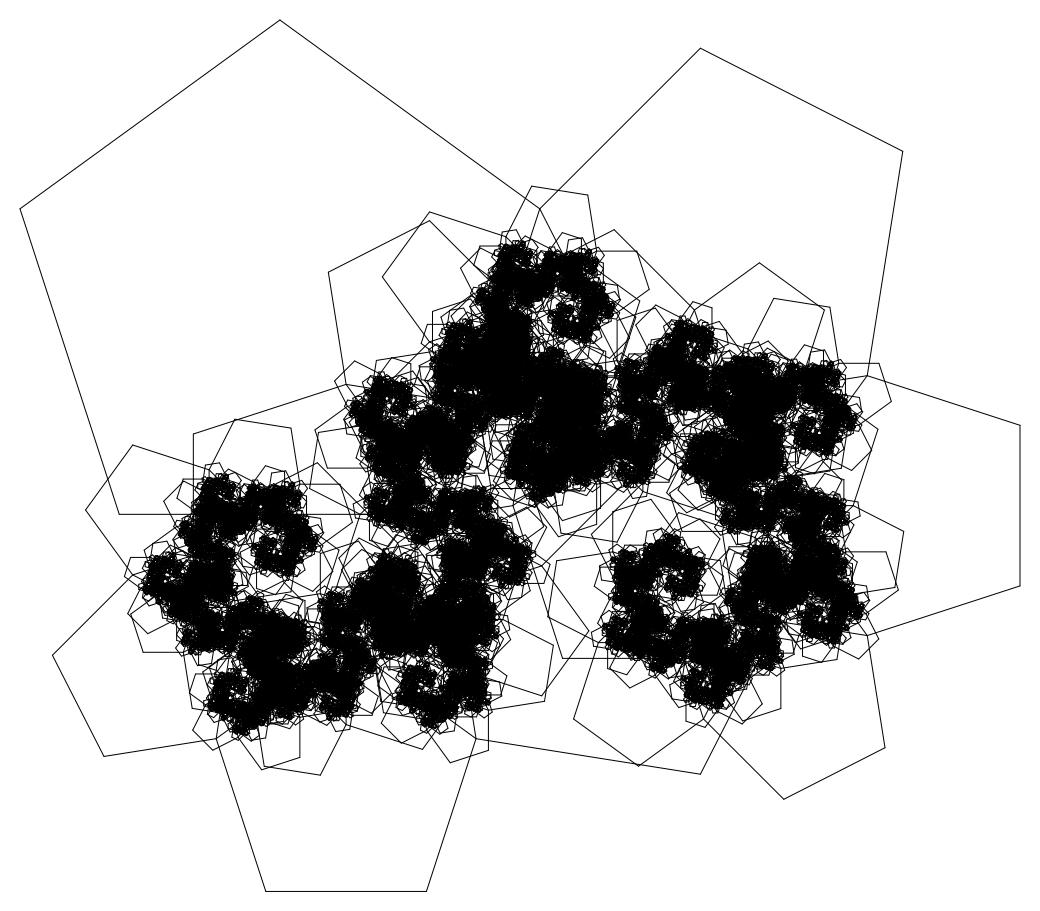
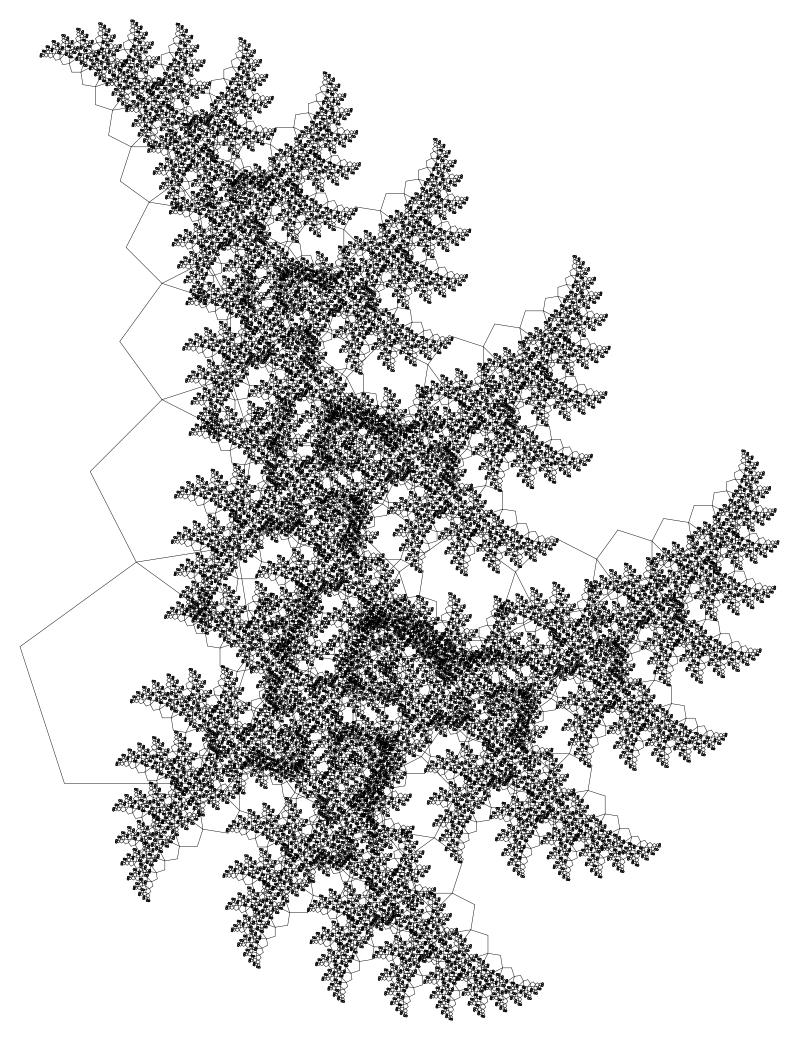
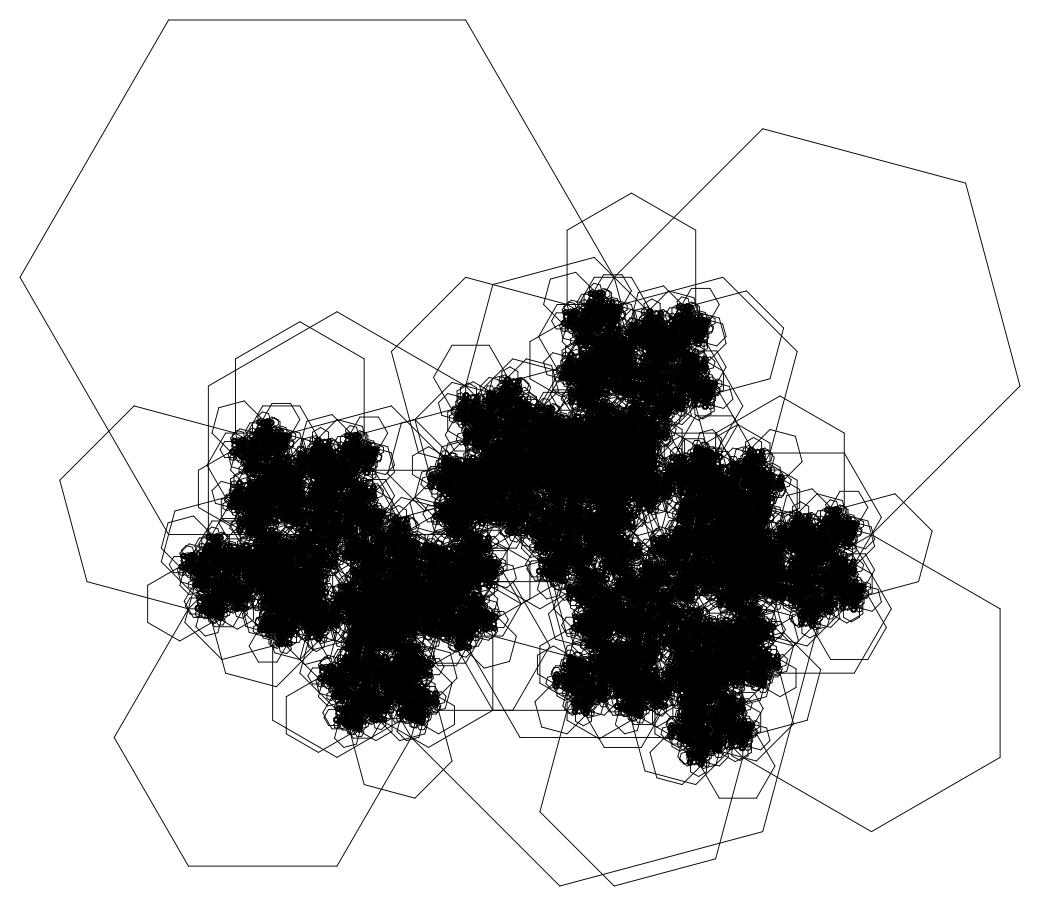


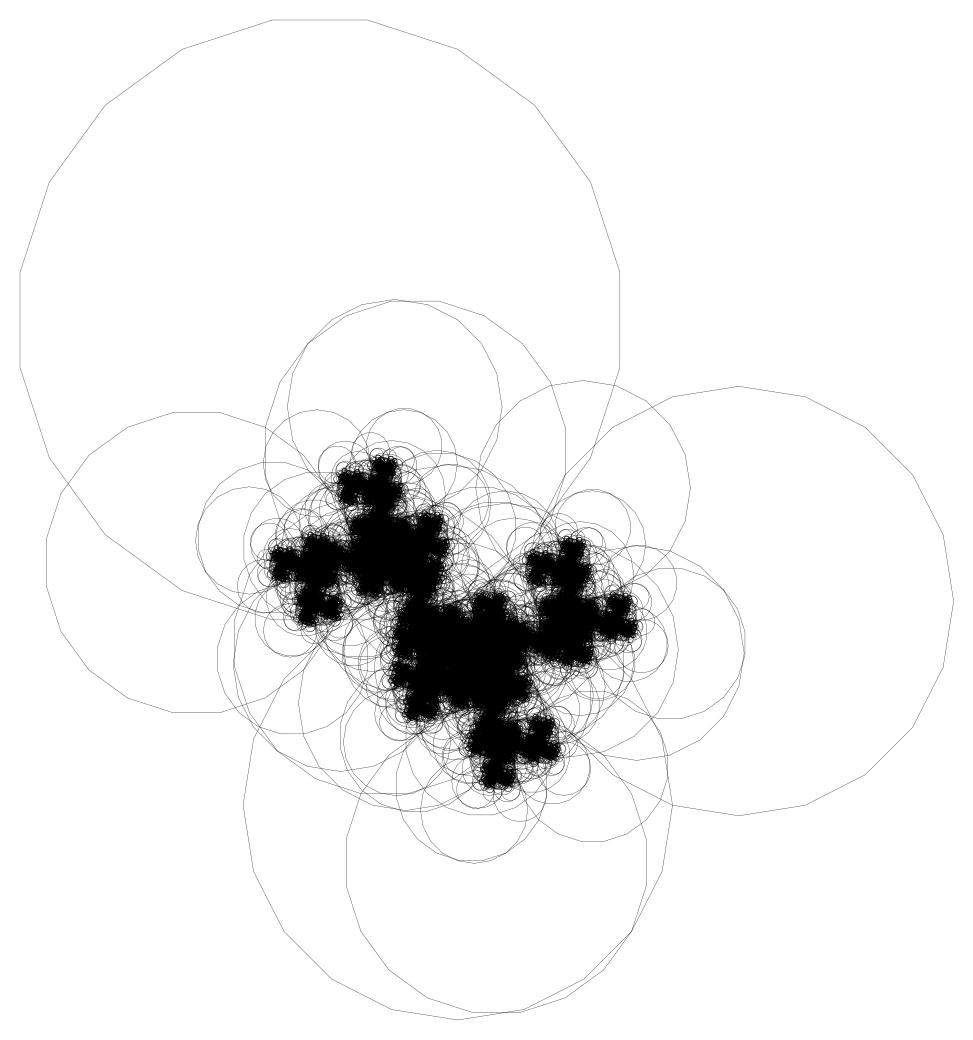




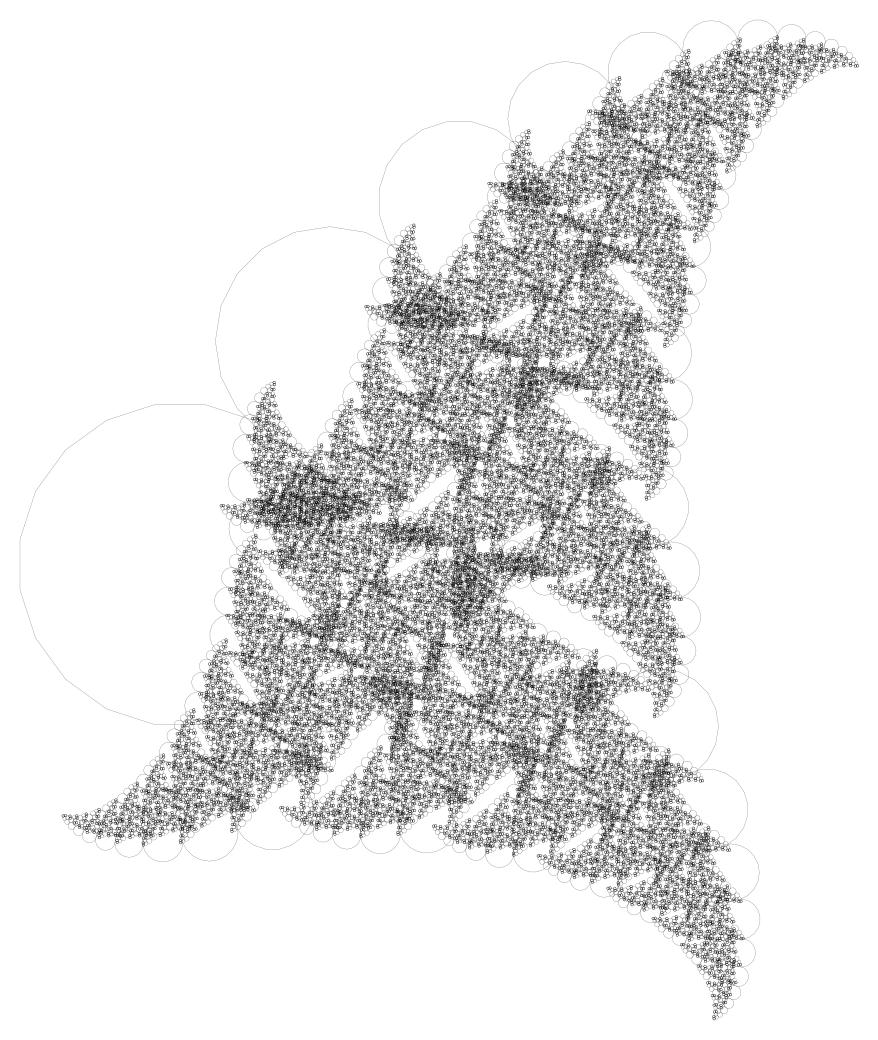


Минусы этого решения:
- Применимо только к правильным многоугольникам.
- Требует ещё более сложных вычислений формул.
- Большинство минусов плохого решения для простого дерева Пифагора.
#2Хороший путь с использованием библиотеки
Это может показаться удивительным, но по сравнению с предыдущим хорошим решением, это совсем немного отличается. Главные отличия: координаты фигуры теперь пишутся не a, b, c, а пишутся в массив. Так же есть строчки для вычисления правильного многоугольника.
void draw_pythagoras_tree(const space2& space) {
// Выходим из рекурсии, если одна из осей (аналогично и сторона квадрата) имеет длину меньше, чем 2
if (space.i.length() < 2)
return;
// Считаем правильный многоугольник
const int n = 5;
const int m = 1;
std::vector<vec2> poly;
for (int i = 0; i < n+1; ++i) {
double angle = deg2rad(360.0/n * i);
poly.push_back(vec2(cos(angle), sin(angle)));
}
// Преобразуем координаты так, чтобы он своим первым ребром находится на оси X
space2 poly_line = makeLine2(poly[0], poly[1]);
poly = toMas(poly_line, poly);
// Высчитываем координаты прямоугольного треугольника, который лежит своей гипотенузой на оси X, с углом alpha при основании
double alpha = spob::deg2rad(45);
std::vector<vec2> triangle = {
vec2(0, 0),
vec2(1, 0),
rotate(vec2(cos(alpha), 0), vec2(0), alpha)
};
// Преобразуем многоугольник из текущих координат к координатам переданного пространства
poly = fromMas(space, poly);
// Рисуем многоугольник
for (int i = 0; i < poly.size() - 1; i++)
draw_line(poly[i], poly[i+1]);
// Строим пространство, которая находится на m-й стороне многоугольника
space2 tr_line = makeLine2(poly[m+1], poly[m]);
// Переводим координаты треугольника к этому пространству
triangle = fromMas(tr_line, triangle);
// Строим пространства, которые находятся на обоих катетах этого треугольника
space2 l1 = makeLine2(triangle[0], triangle[2]);
space2 l2 = makeLine2(triangle[2], triangle[1]);
// Рекурсивно строим дерево в этих пространствах
draw_pythagoras_tree(l1);
draw_pythagoras_tree(l2);
}
Пошаговое объяснение создания многоугольника:
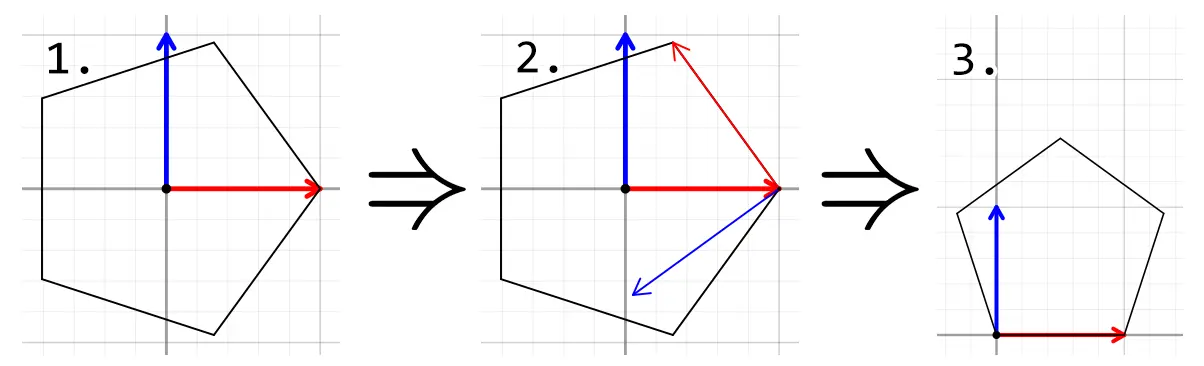
png
- Для начала, самое главное, построение координат правильного многоугольника:
Можно заметить, что это просто вышеописанная формула с Википедии, только максимально упрощенная, без радиуса, без угла смещения. Но к сожалению полученный многоугольник не обладает важным свойством полного нахождения на оси X.const int n = 5; const int m = 1; std::vector<vec2> poly; for (int i = 0; i < n; ++i) { double angle = deg2rad(360.0/n * i); poly.push_back(vec2(cos(angle), sin(angle))); } - Поэтому сначала мы создаем систему координат из первой стороны многоугольника
space2 poly_line = makeLine2(poly[0], poly[1]); - А затем переводим каждую координату этого многоугольника к этой системе координат.
В итоге наш многоугольник полностью находится на оси X, и его можно использовать в построении.poly = toMas(poly_line, poly);
Кстати, абсолютно аналогичным образом можно было и создать треугольник:
std::vector<vec2> triangle = {vec2(0, 0), vec2(cos(alpha), 0), vec2(0, sin(alpha))};
space2 triangle_line = makeLine2(triangle[1], triangle[2]);
triangle = toMas(triangle_line, triangle);
Ведь намного проще понять координаты треугольника заданного так, что прямой угол лежит в центре координат, и все его катеты сонаправлены осям.
Здесь используется функция toMas для сокращения кода. Её действие аналогично следующему:
for (auto& i : poly) i = poly_line.to(i);
Также есть небольшая хитрость: в цикле генерации правильного многоугольника цикл идёт не до n, а до n+1. Сделано это потому что мы не можем зациклить массив, чтобы нарисовать все стороны многоугольника. Поэтому последняя точка является как бы первой.
Немного построения:
А теперь наиболее интересные по моему мнению анимации изменения угла для разных многоугольников:
#Пути дальнейшего развития
#2Обощение
Вообще, все фракталы, что здесь были нарисованы, являются вариацией одного класса фракталов, которые строятся одинаково. Итак, пусть у нас есть некоторый многоугольник. Некоторая его сторона является основанием, так же задано на каких сторонах строить фрактал. Далее рекурсивно осуществляется следующий алгоритм:
Нарисовать многоугольник так, чтобы он своим основанием стоял на заданной системе координат
Получить пространства всех сторон многоугольника, которые заданы
Применить рекурсию ко всем этим пространствам
Тогда для дерева Пифагора этим многоугольником является объединение квадрата и прямоугольного треугольника. Стороны, на которых надо рисовать - катеты треугольника.
Все стороны, по которым надо строить фрактал, должны быть меньше по длине, чем основание. Если они будут больше или равны основанию, тогда фрактал получится бесконечно большим, и с каждой итерацией он может возрастать в размерах.
#2Улучшение эффективности
Вообще данное решение является очень топорным, и работает недостаточно эффективно при маленьких углах. Вот мои старые замеры времени генерации кадра в зависимости от угла при основании прямоугольного треугольника для стандартного дерева Пифагора:
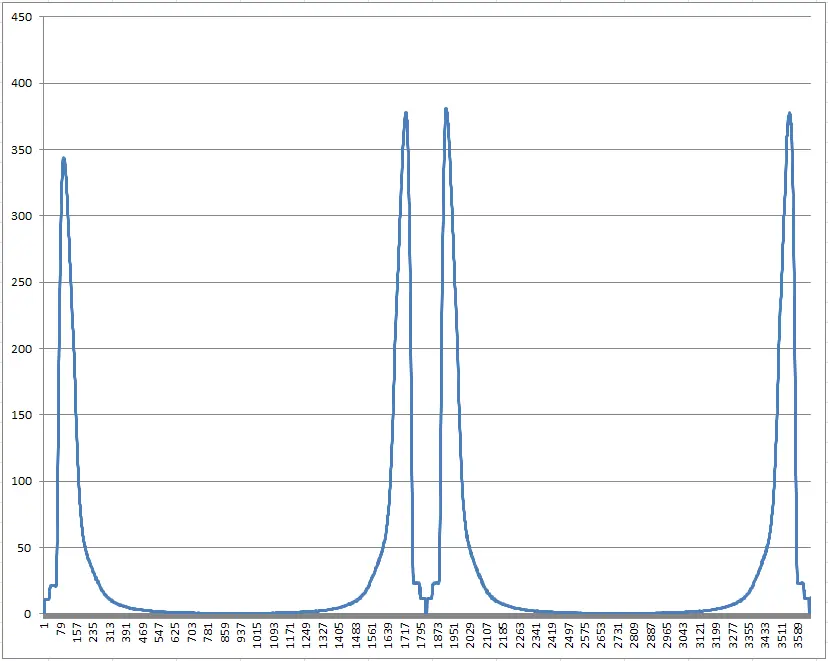
png
Вот такие повышения времени идут когда рисуется при очень маленьком угле, либо угле, близком к 90 градусов. В этом случае дерево выглядит как-то так:
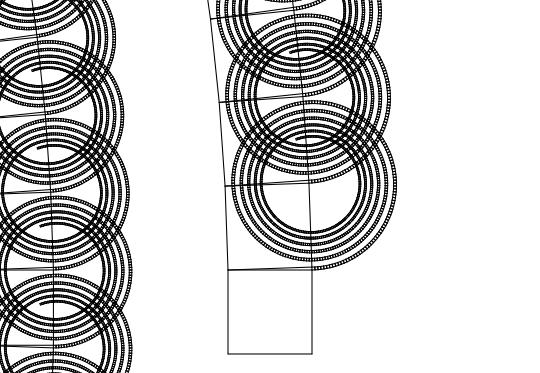
png
Хотя здесь максимальная глубина задана 1000. Такое долгое время вычислений получается из-за того что дерево слишком большое.
Чтобы оптимизировать это, можно пользоваться свойством самоподобности этого фрактала: сначала рисуем его в одно изображение в маленьком разрешении, а затем просто перерисовываем эту картинку, вместо того, чтобы вычислять координаты для каждой ветки и рисовать отдельно каждый квадрат. Затем применяем это как-нибудь рекурсивно, чтобы на каждой итерации увеличивать степень точности изображения.
Но это лишь идея в общих чертах. Она так же применима и к общему решению.
#Выводы
Можно заметить, что в моем коде задача каждый раз решается полностью с нуля, и считается, как будто не существует вообще ничего, кроме этой задачи; и задачу никак не планируется расширять. Вследствие этого, для задачи вычислялись сложные формулы, которые никак, кроме как для этой задачи, не могут быть применены. Это плохой метод, программирование никогда бы не развилось до такого уровня, на каком оно есть сейчас, пользуйся все таким грубым подходом. Так же ничего не было вынесено в какие-то функции для упрощения кода.
А чем кардинально отличается новое решение задачи? Оно повышает уровень абстракции. Если при написании первого решения я думал строго в терминах координат, в терминах формул, которые используют эти координат (на низком уровне), то в новом решении я использую некоторые абстрактные объекты: "системы координат", "векторы" и применяю абстрактную процедуру как "преобразование координат" (а это уже более высокий уровень абстракции). Как видно, код от этого стал намного проще, он не только пишется хорошо, но ещё его способен понять другой человек. Да и в нём вообще не используется каких-либо формул, только понятные человеку имена функций.
Ещё в старом коде при незначительном усложнении задачи (перейти от квадрата к правильному многоугольнку), значительно сильно усложнялся код. В новом же решении понадобилось совсем немного строк для решения новой задачи.
Это и есть суть более высокого уровня абстракции - мы не задумываемся над низкоуровневыми вещами, вроде формул, а мыслим более сложными абстрактными объектами, которые позволяют нам эффективней решать задачу.
Конечно, эта эффективность ещё зависит от того, насколько хорошо написана библиотека. Для некоторых задач незначительное усложнение влечет за собой незначительные изменения, а иногда совсем наоборот.
#Как зарождалась эта библиотека
Поначалу, как вы можете видеть, я вообще не пользовался никакими абстракциями. Потом, в одном проекте графического интерфейса GraphWinApi я создал класс Point, который представлял собой обычный двумерный вектор. Я всего-лишь написал для него тривиальные методы, вроде move, rotate, +, * и т. д., но затем я удивился насколько просто можно рисовать повернутые объекты с использованием функции rotate.
Далее, в библиотеке TinyWindowsGraphics я написал класс PointBase по сути с теми же методами, только немного лучше, плюс методы toBasis, fromBasis. И даже написал код для генерации фрактала на линии с помощью этих функций:
template<class Draw>
void drawFractal(ImageDrawing_aa& img,
Polygon_d& poly, const
Draw& draw,
int8u maxDepth = 30,
double minRadius = 0.5,
int32u depth = 0) {
if (depth < maxDepth && (poly.array[1]-poly.array[0]).getLength() > minRadius) {
draw(poly, depth);
for (int8u i = 0; i < poly.array.size()-1; ++i) {
Polygon_d poly1 = poly;
poly1.move(-poly1.array[0]);
Point_d ox = poly.array[poly.array.size()-1]-poly.array[0];
ox /= ox.getLength();
Point_d oy = ox;
oy.rotate(pi/2.0);
poly1.toBasis(ox, oy);
Point_d nx = poly.array[i+1] - poly.array[i];
nx /= (poly.array[poly.array.size()-1]-poly.array[0]).getLength();
Point_d ny = nx;
ny.rotate(pi/2.0);
poly1.fromBasis(nx, ny);
poly1.move(poly.array[i]);
drawFractal(img, poly1, draw, maxDepth, minRadius, depth+1);
}
}
}
Вообще, я бы мог написать статью об этом решении, но оно не настолько красивое, да и тогда я не осознал всю суть.
Где-то с этого момента я вспомнил линейную алгебру и у меня в голове засела идея, что системы координат неплохо так использовать во множестве задач.
Далее в одном секретном проекте под действием этой идеи родилось понятие системы координат, там преобразование координат было самой основой. Поначалу это было в виде некрасивых функций toCoordSystem(), fromCoordSystem(), затем под множеством волн рефакторинга появилось то, что есть сейчас. Ввиду огромного удобства я начал использовать этот код во всех своих других проектах. И приходилось тащить везде весь код этого секретного проекта только ради преобразований координат. Тогда я и понял, что эта часть является настолько независимой от самого проекта, что должна быть вынесена в отдельную библиотеку.
Ну, и как говорится вначале, когда я начал придумывать примеры для этой библиотеки, я осознал всю её мощь; насколько хорошо она применима к моим старым проектам.
Именно поэтому я и показывал вам весь этот путь от кошмарного кода к коду, использующему абстракции на простом примере одного фрактала.
Повышайте уровень абстракции. До встречи!
