Есть такой алгоритм, называется «метод Ньютона». Предназначен он для численного решения уравнений вида f(x)=0. Так же есть фрактал под названием «бассейны Ньютона», почитал я об этом и решил тоже нарисовать их, только не на комплексной плоскости, а для действительных чисел.
Тогда возникает вопрос: как это нарисовать, если для действительных чисел будет 1D картинка? Ответ: использовать системы уравнений и многомерный метод Ньютона! Я даже как-то писал о нём статью (ссылка на репозиторий).
Как и обычный, так и многомерный метод Ньютона умеет находить только один корень, и к какому корню он сойдётся, зависит по большей части от начального приближения. Бассейны Ньютона визуализируют к какому корню придёт метод, если начать с этой точки, показывая это цветом.
Вот так выглядят бассейны Ньютона для системы уравнений, которая находит точки пересечения двух окружностей:

png
Что-то очень скучно :D, никаких фракталов. Ладно, попробуем увеличить сложность:
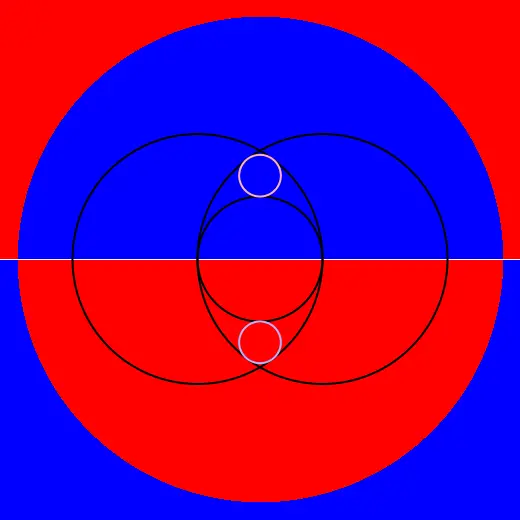
png
Здесь система уравнений из трёх уравнений по нахождению касательной к трём окружностям. На картинке показана зависимость только от положения начального приближения, но на самом деле есть зависимость и от радиуса, но для неё надо 3D картинку рисовать. В целом, там ничего особенного не наблюдается.
Это всё интересно, но я хочу увидеть фракталы! И я смог, на функциях с 3 степенью. Вблизи точки пересечения, то есть корня, всё хорошо, но на пограничных областях возникают фракталы, и без всяких комплексных чисел!

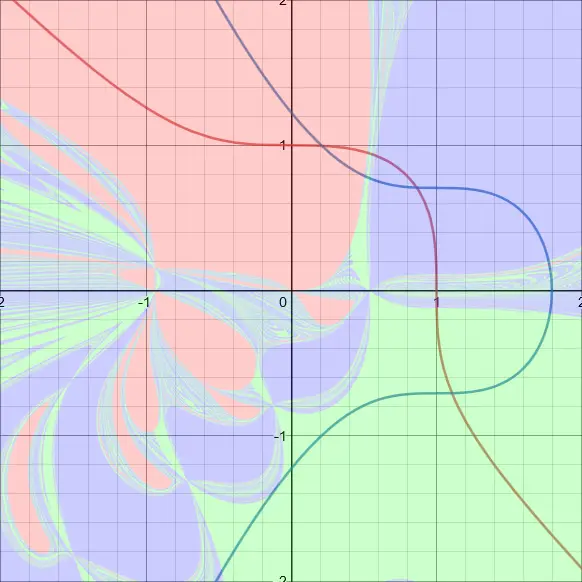

Таким образом теперь вы знаете ещё одну область из реальной жизни, где возникают фракталы.
UPD: В 2021 вышло отличное видео от 3Blue1Brown по фракталам в методе Ньютона, советую заценить:
Изначально данная статья была опубликована как трэд в твиттере.

