Всем известно про такой клеточный автомат, как "Conway's Game Of Life".
У этого автомата есть такое свойство как необратимость, то есть у данного расположения клеток может быть от 0 до бесконечного числа предков, которые приводят к этому состоянию. Состояния, у которых не может быть предка, называются Садом Эдема.
Легко понять что этот автомат необратим: в нём возможно создать состояния, приводящие к пустому пространству. Очевидно, у пустоты существует бесконечное число предков.
Для устранения этого свойства придумали обратимые клеточные автоматы, то есть у такого автомата всегда может быть потомок и причём только один, и его можно легко алгоритмически вычислить.
По сути такой автомат позволяет заглянуть в прошлое, если нам известно настоящее!
По этим автоматам очень мало информации в сети, из-за чего они меня так сильно заинтересовали. Пример такого автомата - Critters. Алгоритм его работы такой: без пересечений смотрятся все квадратики 2x2 и заменяются согласно трансформации на вики. Затем сетка квадратиков смещается на 1 по диагонали и делается то же самое. Теперь считается что прошёл один шаг и сетка снова двигается на 1 по диагонали (возвращается в прошлое состояние).
Введу пару обозначений:
0- текущее состояние,10- симуляцию10шагов вперёд от текущего состояния,-10- симуляцию10шагов назад.
Меня интересовало в этом автомате:
- как будет выглядеть
-10, если я что-то нарисую в0; - как будет выглядеть
0, если просимулировать до10, затем там что-то модифицировать, а затем просимулировать обратно.
По этим автоматам информации в сети настолько мало, что я не смог найти симуляцию Critters. Поэтому пришлось писать программу самому.
Быстренько накидал программку и выложил на github:critters.
Так эволюционируют криттерсы при обычной симуляции вперёд из рисунка hi.
А вот эволюция рисунка hi в обратную сторону.
Сверху показано текущее состояние поля. Снизу показано как будет выглядеть поле, если его симулировать до 0 шага. Сначала происходит симуляция до 95 шага. Видно, что поле снизу остаётся неизменным. Но, затем я начинаю менять поле в настоящем, удаляя белые точки в некоторых местах. Видно, что от удаления одного глайдера или пары пикселей сразу сильно меняется прошлое. Причём эффект взрывной, ломается целая конструкция.
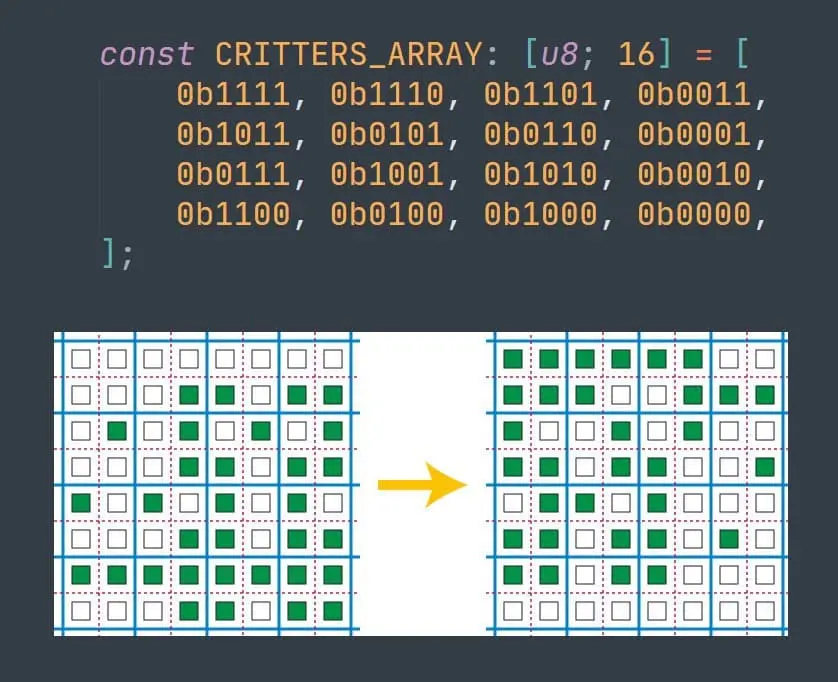
Здесь показано как выглядят правила преобразования с википедии, и как они записаны у меня в программе. Массив для обратной симуляции вычисляется из этого. Вообще любая перестановка этого массива тоже является обратимым клеточным автоматом, наверное среди всех этих перестановок можно найти что-то интереснее.
jpg
Пример одной из перестановок, данного массива.
Я сделал этот автомат на зацикленном поле, следовательно количество состояний конечно, и ограничено 2^(WxH). А учитывая что у любого состояния всегда существует один потомок и один предок, любое состояние через какое-то количество шагов обязательно вернётся в самого себя. Таким же образом можно объяснить почему при применении одной и той же комбинации для Кубика Рубика, он всегда вернётся в изначальное состояние, через определённое число шагов. Таким же образом, если наш мир является конечным обратимым автоматом, то через определённое число больших взрывов и схлопываний он полностью повторит сам себя (напоминает одну серию в Футураме :) ).
Ещё этот автомат не может потерять информацию, потому что он должен быть обратимым. Что это значит можно объяснить на примере: допустим, вы захотели сделать на этом конечном автомате устройство для умножения двух чисел. Тогда такое устройство должно уметь симулироваться обратно, а значит оно должно уметь получать для одного числа два других, которые при умножении дали это число. Но самого числа будет недостаточно, нужна будет ещё мета-информация или "мусор", чтобы вернуться в изначальное состояние. Скорее всего этот "мусор" будет кучей глайдеров, которые вышли из устройства умножения в процессе. Так что взломать RSA не получится)) Кстати, существуют обратимые языки программирования! Пример: Janus.
В "Игре Жизнь" при создании устройства умножения никаких глайдеров не вылетает, всё работает очень чисто, и после умножения устройство может вернуться в изначальное состояние. Это потому что данный автомат теряет информацию.
А наш мир можно симулировать в обратную сторону? Я слышал, что согласно классической механике, да. Насчёт квантовых эффектов уже не уверен. Кстати, в физике существует такая проблема как исчезновение информации в чёрных дырах.
На гифках видно, что critters выглядит довольно скучно в динамике, не сравнимо с тем как красиво выглядит "игра жизнь". Возможно правила не очень удачные, но мне кажется главная проблема что critters не может терять информацию, поэтому его эволюция выглядит так скучно, и вообще там толком не происходит эволюции, просто шум шумит, благо хотя бы глайдеры существуют.
Хотя если учесть что наш мир тоже обратим, то он выглядит слишком интересно. Думаю всё дело в том, что с первого взгляда он выглядит как "игра жизнь", но при более внимательном взгляде весь "мусор", нужный чтобы симулировать его обратно, хранится в виде тепла и электромагнитного излучения. Причём интересные состояния (атомы) сильно влияют на мир, а неинтересные состояния нужные для сохранения информации (тепло, электромагнитное излучение, фотоны), мало влияют на мир. Видимо надо тоже пытаться проектировать клеточный автомат, который всю скуку будет преобразовывать в слабые состояния, а самое интересное в сильные состояния.
В общем я немного разочарован с этим автоматом, его прошлое не интересно, будущее тоже, видимо надо придумывать более сложный автомат с большим числом состояний у одной клетки, может как-то воспользоваться идеей из прошлого абзаца.
