png
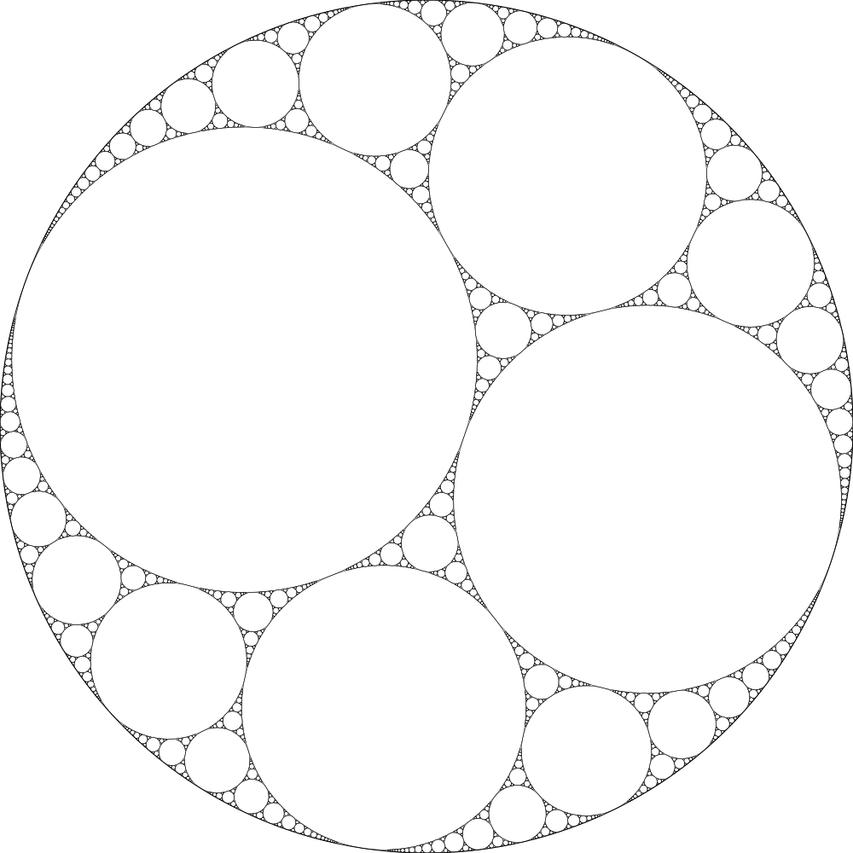
Этот фрактал основан на бесконечном построении касающихся окружностей.
Суть этого фрактала заключается в следующем: изначально у нас есть минимальный набор окружностей (три), у которого мы знаем положение центров и радиусы. Далее необходимо строить касательную к каждой из них, и к каждой из образовавшихся, и так до бесконечности, чтобы пространство полностью заполнялось без пересечений окружностей.
png
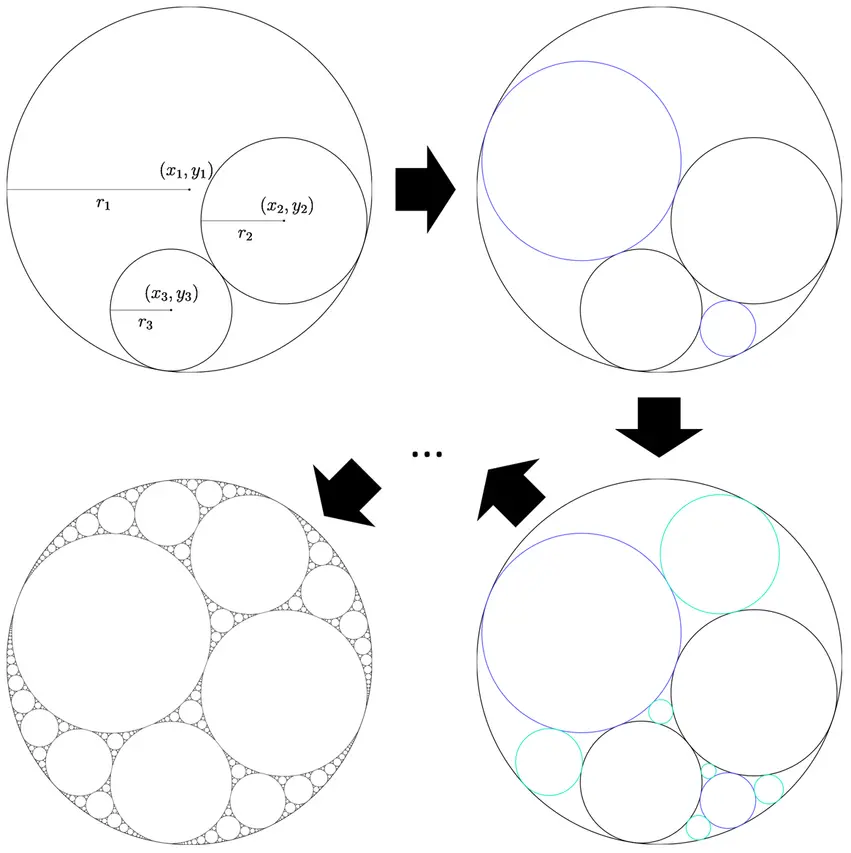
Поэтому, для того, чтобы нарисовать при помощи программы такой фрактал, необходимо сначала решить простую задачу:
Как, зная координаты центра и радиус трех окружностей, найти все касательные к ним?
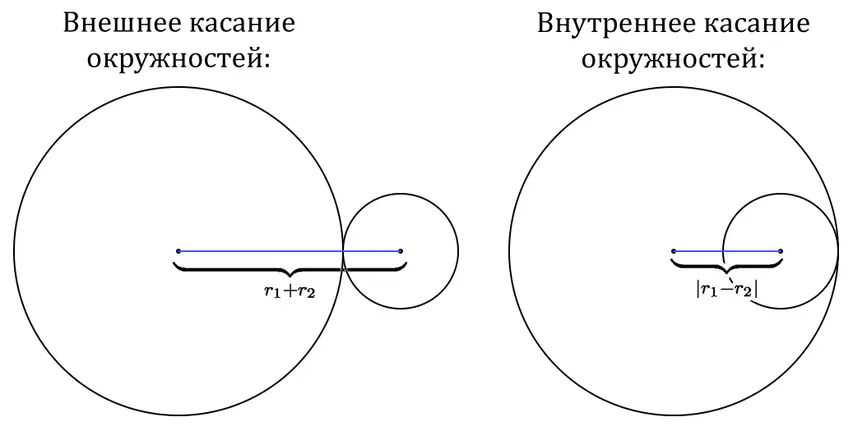
Но для начала свойство двух касательных окружностей: если касание внешнее, то расстояние между центрами окружностей равно сумме их радиусов; если касание внутреннее, то расстояние между центрами равно разности их радиусов, взятое по модулю.
png
Учитывая, что окружностей три, а каждая может касаться четвертой двумя способами, получаем всего 2³=8 способов как могут касаться три окружности с четвертой, которую надо найти.
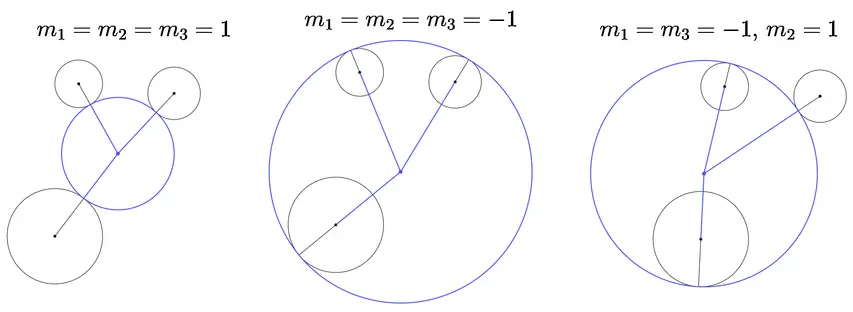
Благодаря этому свойству можем составить систему из трех уравнений, где есть три неизвестных. За m1, m2, m3 я обозначил параметры - внешнее или внутреннее касание для конкретной окружности: +1 означает внешнее касание, -1 внутреннее (рисунок 4).
Благодаря этому свойству можем составить систему из трех уравнений, где есть три неизвестных. За m1, m2, m3 я обозначил параметры - внешнее или внутреннее касание для конкретной окружности: +1 означает внешнее касание, -1 внутреннее.

png
Такую систему уравнений надо как-то решить. Поначалу она может показаться страшной, и на самом деле так и есть :) И проще её решить аналитически, чем при помощи всяких численных методов. Но это аналитическое решение не способна выдать ни одна система символьных вычислений, а если может, то ей не хватит памяти, либо формула выходит километровой, и ее невозможно использовать в программе (если вы найдете такую программу, которая сможет решить эту систему, и там не будет километровой формулы, то я скинусь вам на шаурму). Поэтому единственный доступный способ - решать на бумажке, делая огромное число замен.
png
Пример решения системы уравнений для различных m
Я не буду здесь приводить решение, потому что это слишком сложно: я ещё в школе пытался решить эту систему, но так и не смог; лишь после двух курсов в университете, мои мозги достаточно подготовились, чтобы решить ее до конца. Если захотите повторить мой подвиг, то вот вам подсказка: делайте больше замен, заменяя некоторые части на новые переменные.
Одна очень важная деталь, которую я выяснил насчет решения: оно численно неустойчиво даже для вещественных чисел двойной точности (это при том, что там вычисляются только формулы!), поэтому я использовал библиотеку для длинной арифметики boost::multiprecision::cpp_bin_float, где задал размер вещественного числа в 40 байт (320 бит).
Далее, имея функцию нахождения касательных окружностей к трем данным, можно легко написать функцию, которая из изначального набора строит весь фрактал. В этой функции будет использоваться рекурсия, а так же там надо учесть, чтобы не возникали окружности, которые уже рисовались.
Таким образом получается первая картинка.
Ну а на следующей картинке показаны первые эксперименты: внутрь всех окружностей была вписана изначальная окружность.
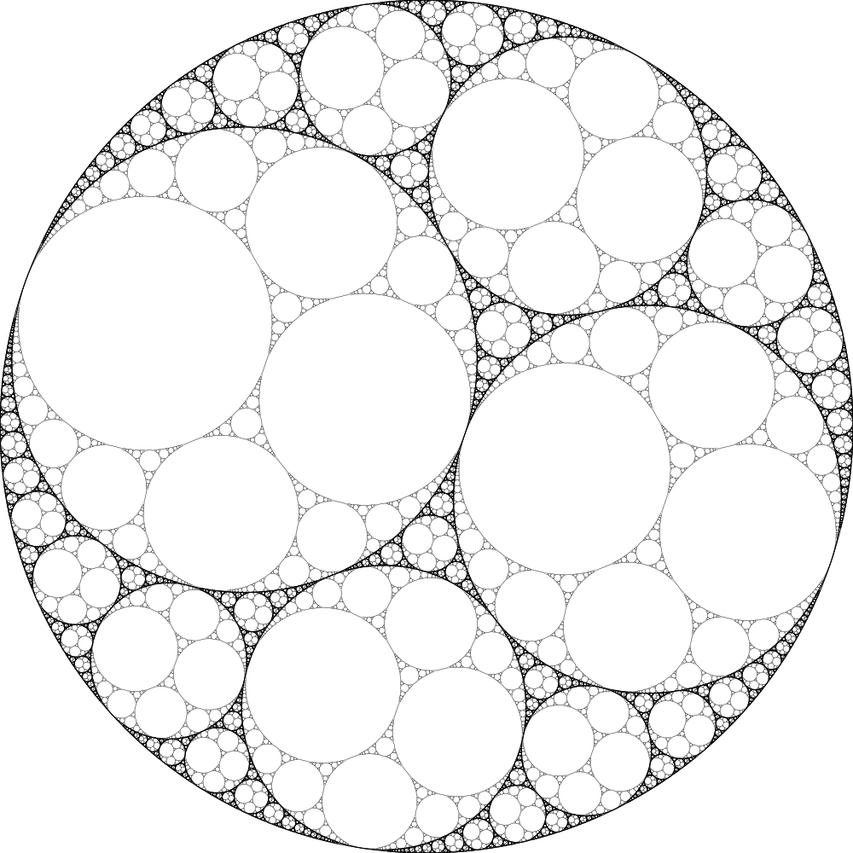
png
А на следующей картинке такой процесс повторялся до бесконечности (причем, чтобы выглядело красиво, цвет более глубоких итераций ставился на более блёклый).
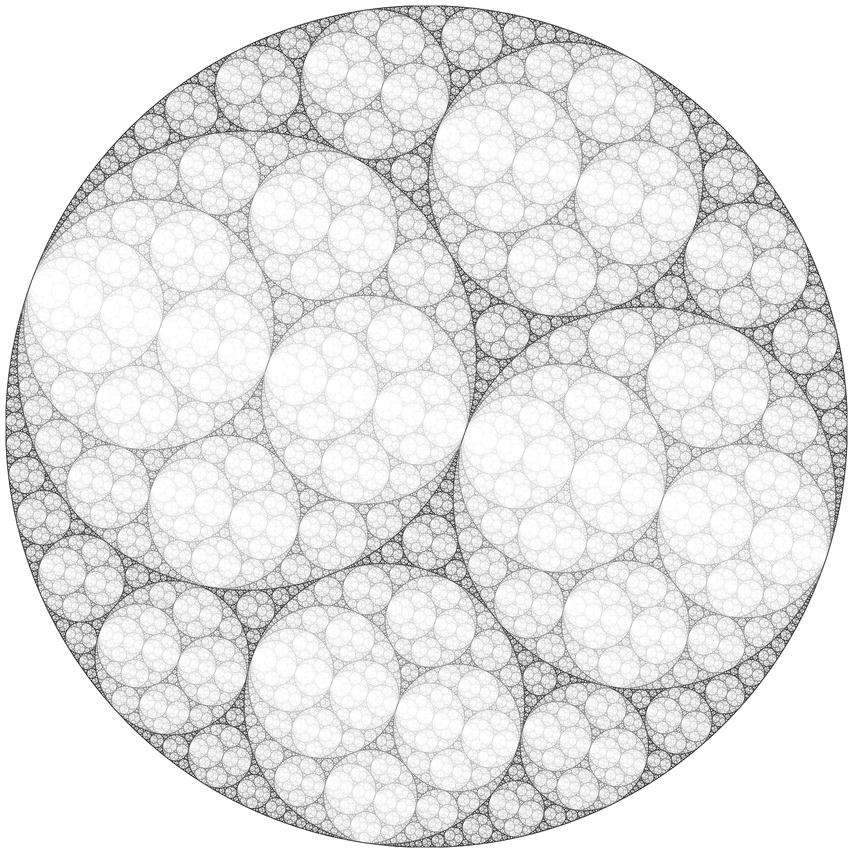
png
Далее планируется переписать код, чтобы он стабильно работал для всех случаев, когда может происходить деление на ноль; вообще создать целую библиотеку вычислений касательных окружностей для разных случаев; создание различных анимаций; создание кругов Аполлона со случайными характеристиками на всех уровнях.
Если у вас появятся идеи того, что ещё можно натворить с кругами Аполлона — предлагайте их в комментариях.
