#Геометрия Лобачевского (гиперболическая геометрия)
Далее кратко будет называться просто гиперболика.
2D пространство с гиперболической геометрией обозначается как H2, аналогично 3D как H3. Обычное евклидово пространство обозначается буквой E, например: E, E2, E3, E4.
Здесь будет систематизироваться интересный материал из чатика: https://t.me/metageometria
#Теоремы и аксиомы этой геометрии
В обычной евклидовой геометрии есть 5 аксиом, из которых выводится всё остальное. И среди них есть пятая аксиома:
На плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной.
В гиперболике эта аксиома отрицается:
Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.
Ещё раз: здесь параллельные прямые не пересекаются! Они пересекаются в сферической геометрии.
Из этой аксиомы следует что через данную точку проходит бесконечно много прямых, не пересекающих данной. Изображается это так:
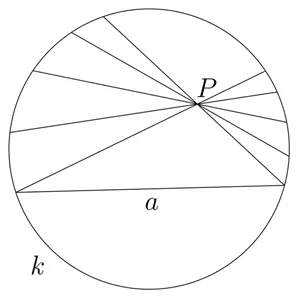
png
Так же есть изображения, хорошо показывающие основные различия всех трёх известных геометрий:
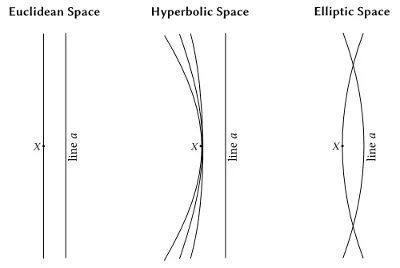
png

png
#Книги
Книга Атанасян Л.С. Геометрия Лобачевского
Книга Прасолов В.В. Геометрия Лобачевского
#Визуализация
Если подумать: как нам визуализировать евклидову геометрию? Да очень легко! Просто берём 2D листок и рисуем на нём, ведь наш мир евклидовый! А гиперболическую геометрию так легко не получится, для неё надо придумывать особые проекции, которые искривляют прямые линии в округлые. Аналогично как перспективная проекция изменяет расстояния и размеры для трёхмерных объектов.
#2Диск Пуанкаре
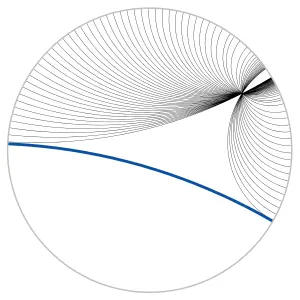
png
#2Верхняя полуплоскость
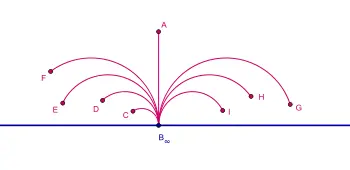
png
Прямая представляется как полу-окружность, с центром на прямой y=0. Так, чтобы построить прямую по двум точкам, надо построить окружность по этим двум точкам. Благо ограничение с центром на прямой сокращает число неизвестных до двух. Либо это вертикальный луч.
Гиперболические окружности проецируются как окружности, но координаты центра и радиус рассчитываются по-другому: (x, y cosh(r)), r = y sinh(r)
Преобразование в диск пуанкаре делается с помощью cayley transform
Я даже визуализировал это здесь и здесь (немного другое преобразование для красоты).
#2Band model
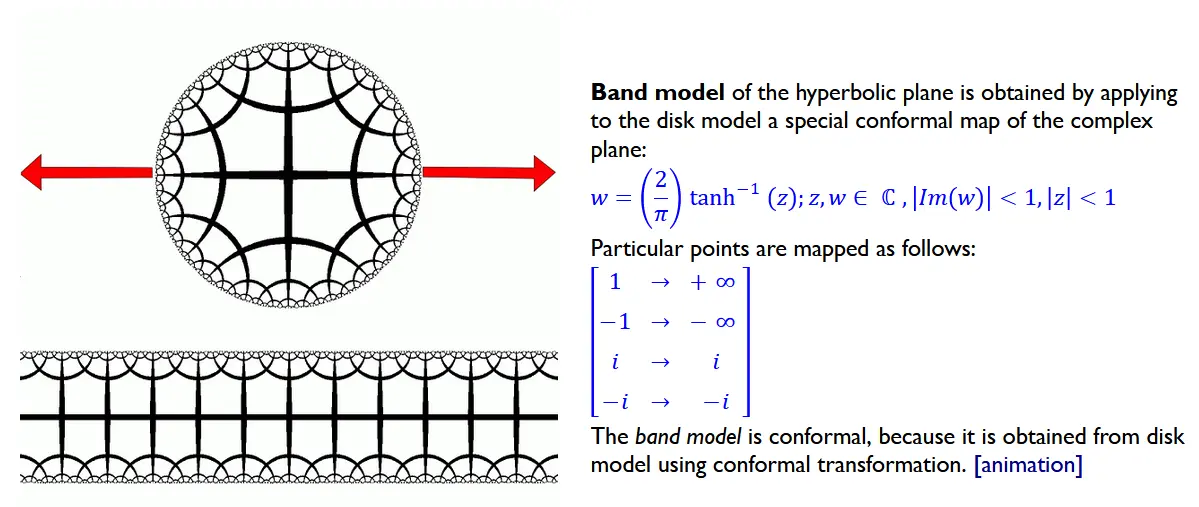
png
#2Рейтрейсинг
А вот чтобы изобразить H3, можно использовать те же методы, что и для визуализации E3, например: перспективную проекцию и рейтрейсинг. Что, собственно, и сделали в следующем видео:
#2А что если
А что если спроецировать H3 при помощи перспективной проекции на кусок H2. Будут ли там прямые линии прямыми? Да и вообще, какая проекция H3 на H2 обладает максимальным количеством хороших свойств?
#Вычисления
Zeno Rogue советует эту стаью для расчётов в гиперболическом пространстве.
#2С чего я начинал
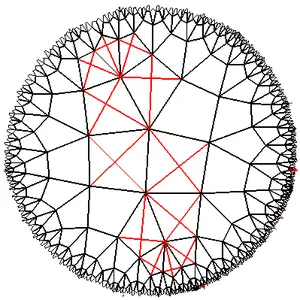
gif
Статья, где очень хорошо объясняют как симулировать плоскость Лобачевского: Жизнь на плоскости Лобачевского . В ней есть ещё много чего интересного, например замкнутость пространства на самого себя, надо это изучить.
При помощи неё я нарисовал своё первое замощение и гифки интерполяции между моделью верхней полуплоскости и диска пуанкаре.
#2Движение на диске Пуанкаре

png
А чтобы двигаться по оси с произвольным углом, надо просто перемножить эти матрицы так:
если обозначить первую матрицу как M(x), вторую как R(ф), то надо сделать матрицу
R(ф) * M(x) * R(-ф)
Анимация движения под 45 градусов.
#Замощения
Вы, наверное знаете, что обычное двумерное пространство можно замостить правильными многоугольниками:

png
В гиперболической геометрии на это есть куда больше свободы, потому что там у любого правильного многоугольника может быть почти любой угол: в зависимости от размера, угол уменьшается.
Происходит так потому что из 5 аксиомы следует, что треугольники равны, если равны их углы. В обычной же геометрии треугольники подобны, если равны углы. Из этого следует, что в гиперболике не существует подобия, и углы правильного многоугольника однозначно определяют его размеры.
За счёт этого можно разгуляться со всякими замощениями, изменяя размер фигур. Например у этого замощения угол в правильных пятиугольниках равен 90 градусов:
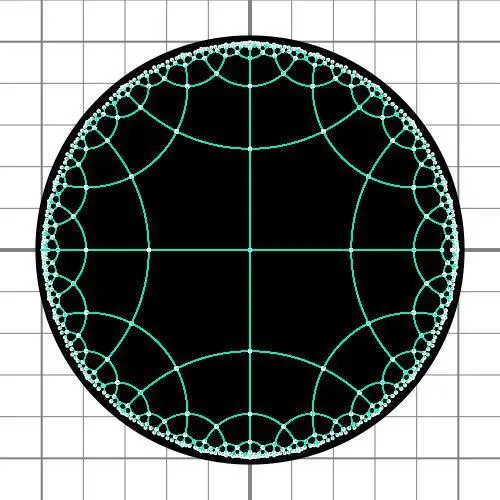
jpg
Лекция про замощения на гиперболической плоскости:
#Игра на гиперболике
#2Майнкрафт
У меня есть желание сделать майнкрафт в H3, используя замощение пространства кубами {4, 3, 5}.
Сначала была идея сделать по горизонтальной плоскости H2, а по высоте -- обычное E, чтобы по высоте работало привычно нашему восприятию, то есть пространство H2×E. Но потом я понял, что это выглядит очень некрасиво: дальние предметы выглядят сжатыми по горизонтали и очень высокими. Выглядит это так:
VR implementation of H^2 x E geometry
Поэтому я решил, что это выглядит некрасиво, и я хочу сделать майнкрафт в пространстве H3. Гравитация там будет направлена по перпендикуляру к полу. Пол проведу примерно так.
Рендерить это можно при помощи рейтрейсинга.
#2Ограничения по памяти
Если в привычном нам евклидовом мире площадь окружности возрастает пропорционально квадрату от размера окружности, то в гиперболическом пространстве всё намного хуже:
Согласно этому источнику, там площадь окружности возрастает как:
S = 4 pi sinh2(r/2).
Для тех кто не знает, гиперболическй синус вычисляется так:
sinh(x) = (ex - e-x)/2.
А это значит что площадь окружности растёт примерно пропорционально квадрату экспоненты, а это очень много.
Если мы хотим хранить мир майнкрафта в виде блоков, то уже для окружности радиуса 30 у нас будет так много блоков внутри, что это не поместится ни в одну память персонального компьютера. К слову, для такого же количества блоков в евклидовом майнкрафте нам потребуется окружность радиуса 32 миллиона блоков.
Поэтому в гиперболическом майнкрафте мы не можем позволить себе такое удовольствие как генерация мира с возможностью его изменять. Нам придётся ограничиться:
- либо плоским миром, где пользователь может поставить конечное число блоков;
- либо автогенерируемым миром, в котором нельзя ничего поменять.
Второй пункт выбрала игра HyperRogue, но она находится на 2D плоскости.
#2Сжатость
Длина границы окружности в гиперболическом пространстве тоже измеряется через экспоненту:
L = 2 pi sinh(r)
А это значит, что на расстоянии 20 у нас будет помещаться примерно e20 блоков, следовательно вдалеке мы будем видеть мир очень сжатым. И движение по такому миру будет выглядеть не как обычное движение, а как зумирование, ведь всё будет очень быстро увеличиваться в размерах.
#Интересности
#2Дискретные координаты для замощений на гиперболической геометрии
Это три связанных статьи:
What does it mean to introduce coordinate system on a regular tiling?
Coordinate system for heptagonal tiling of hyperbolic plane
Adjacent heptagons on hyperbolic plane
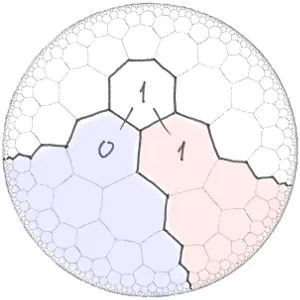
png
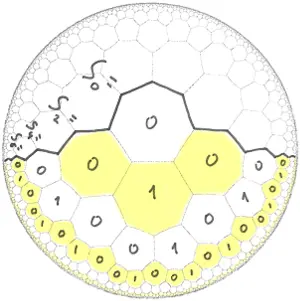
png
Тоже что-то про дискретные координаты, чтобы не потерять
#2Демки на гиперболической плоскости
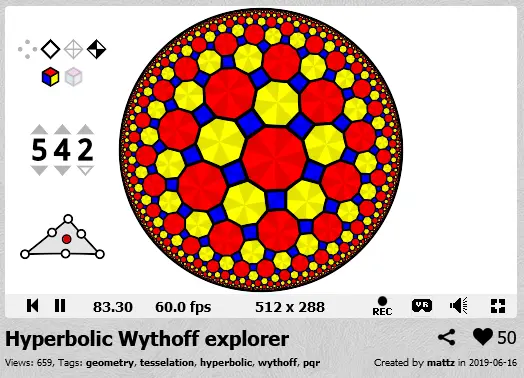
png
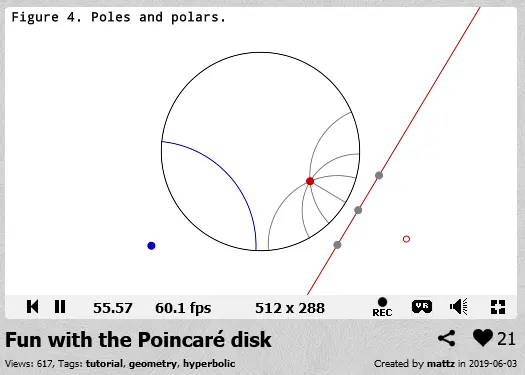
png

png
Анимация движения объектов в замощении квадратами:
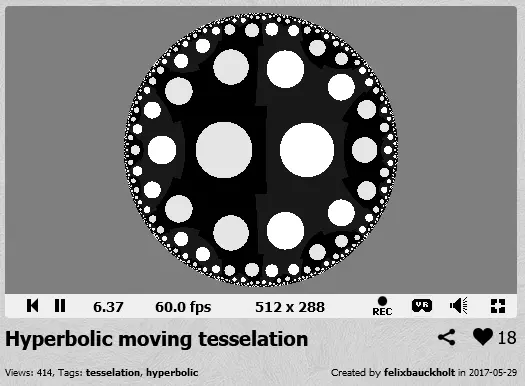
png
#Мемы

jpg
jpg
#Несортированные ссылки
Крутая презентация про мапинг гиперболического пространства на разные фигуры.
Статья с множеством примеров игр и визуализаций гиперболического пространства.




Changelog
2021.08.26
Перевод этой страницы на новый блог на Zola.
2020.11.16
Перевод этой страницы на submodules + jekyll.
2020.01.06
Первая публикация.